The energy dissipated by a resistor is 10 mj in 1 s when an electric current of 2 mA flows through it. The resistance is ______Ω (Round off to the Nearest Integer)
To find the resistance of the resistor, we can use the formula for electrical energy dissipated in a resistor, which is given by:
H=I2RT
Where:
- H is the energy dissipated (in joules),
- I is the current (in amperes),
- R is the resistance (in ohms),
- T is the time (in seconds).
Step 1: Convert the given values into standard units
- The energy dissipated H is given as 10 mJ, which is:
H=10 mJ=10×10−3 J=0.01 J
- The current I is given as 2 mA, which is:
I=2 mA=2×10−3 A=0.002 A
- The time T is given as 1 second:
T=1 s
Step 2: Rearrange the formula to solve for resistance R
From the formula H=I2RT, we can rearrange it to find R:
R=HI2T
Step 3: Substitute the known values into the formula
Now, substituting the values we have:
R=0.01 J(0.002 A)2×1 s
Step 4: Calculate I2
Calculating I2:
I2=(0.002)2=0.000004 A2
Step 5: Substitute I2 back into the equation for R
Now substituting I2 back into the equation:
R=0.010.000004×1=0.010.000004
Step 6: Perform the division
Calculating the division:
R=0.010.000004=2500Ω
Step 7: Round off to the nearest integer
Since the question asks for the resistance rounded off to the nearest integer, we have:
R≈2500Ω
Final Answer
The resistance is 2500Ω.
---
- H is the energy dissipated (in joules),
- I is the current (in amperes),
- R is the resistance (in ohms),
- T is the time (in seconds).
- The energy dissipated H is given as 10 mJ, which is:
H=10 mJ=10×10−3 J=0.01 J
- The current I is given as 2 mA, which is:
I=2 mA=2×10−3 A=0.002 A
- The time T is given as 1 second:
T=1 s
From the formula H=I2RT, we can rearrange it to find R:
R=HI2T
Now, substituting the values we have:
R=0.01 J(0.002 A)2×1 s
Calculating I2:
I2=(0.002)2=0.000004 A2
Now substituting I2 back into the equation:
R=0.010.000004×1=0.010.000004
Calculating the division:
R=0.010.000004=2500Ω
Since the question asks for the resistance rounded off to the nearest integer, we have:
R≈2500Ω
The resistance is 2500Ω.
Similar Questions
Knowledge Check
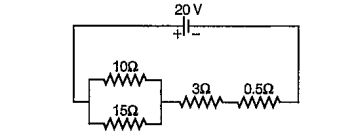
In the circuit, the current flowing through 10Ω resistance is
 A12AB1.2AC0.8AD0.4A
A12AB1.2AC0.8AD0.4AA voltmeter of resistance 1000Ω gives full scale deflection when a current of 100mA flow through it. The shunt resistance required across it to enable it to be used as an ammeter reading 1A at full scale deflection is
A10000ΩB9000ΩC222ΩD111Ω
A current of 200mA flows through a 4kΩ resistor. What is the p.d. across the resistor?
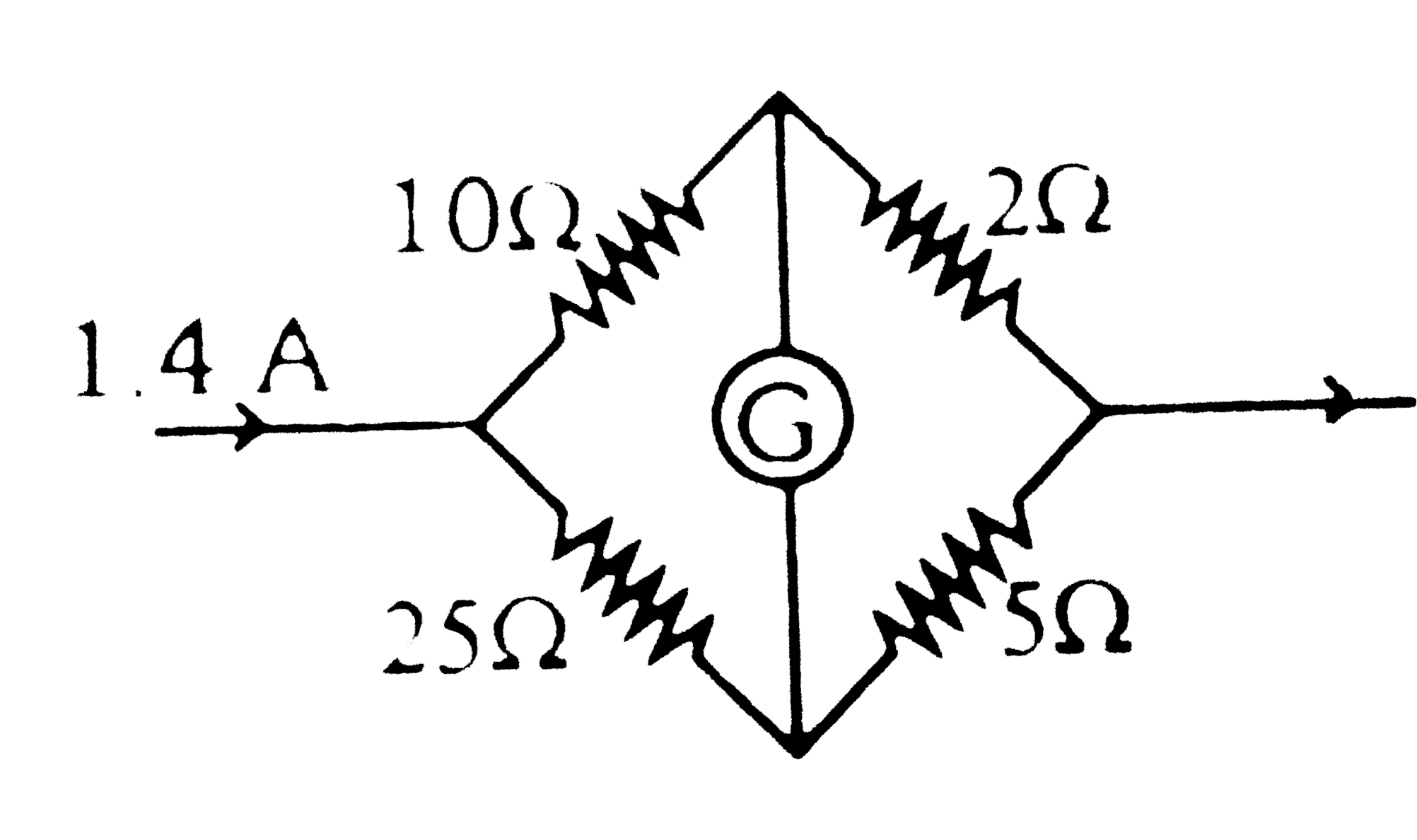
View SolutionIn the figure given, the electric current flowing through the 5 kn resistor is 'x’ mA.
The value of x to the nearest integer is _________
View SolutionFind resistance if it dissipates 10 mJ of energy per second when current of 1 mA passes through it
View SolutionCurrent 2 A is flowing through a conductor fo resistance 4 Ω . Find the electrical energy consumedin 10 s.
View SolutionAn electric current of 4.0A flows through a 12Ω resistor. What is the rate at which heat energy is produced in the resistor?
View SolutionA transistor is connected in common emitter circuit configuration, the collector supply voltage is 10 V and the voltage drop across a resistor of 1000 Ω in the collector circuit is 0.6 V. If the current gain factor (β) is 24, then the base current is _______ μA. (Round off to the Nearest Integer)
View Solution