The energy of an oscillating body in simple harmonic motion depends on its mass , frequency and amplitude using the method of dimensional analysis find the relation between E ,m, n and a .
The correct Answer is:D
To find the relation between energy E, mass m, frequency n, and amplitude a using dimensional analysis, we can follow these steps:
Step 1: Identify the dimensions of energy
Energy E can be expressed in terms of force and displacement. The dimensional formula for force is given by:
Force=mass×acceleration=m⋅(lengthtime2)=m⋅LT2
Thus, the dimensions of force are:
(F)=MLT−2
Energy is defined as force multiplied by displacement:
E=Force×Displacement=F⋅L
So, the dimensions of energy are:
(E)=(F)⋅(L)=MLT−2⋅L=ML2T−2
Step 2: Express energy in terms of m, n, and a
We assume that energy E can be expressed as:
E∝manbac
where a, b, and c are the powers to which mass, frequency, and amplitude are raised, respectively.
Step 3: Write the dimensions of m, n, and a
- The dimension of mass m is:
(m)=M
- The frequency n is the reciprocal of time, so its dimension is:
(n)=T−1
- The amplitude a is a length, so its dimension is:
(a)=L
Step 4: Substitute the dimensions into the equation
Substituting the dimensions into the expression for energy gives:
ML2T−2=(Ma)⋅(T−b)⋅(Lc)
This can be rewritten as:
Ma⋅Lc⋅T−b
Step 5: Equate the dimensions
Now, we equate the coefficients of M, L, and T from both sides:
1. For mass M:
a=1
2. For length L:
c=2
3. For time T:
−b=−2⟹b=2
Step 6: Write the final relation
From the values of a, b, and c, we can write the relation for energy:
E∝m1n2a2
or simply:
E=k⋅m⋅n2⋅a2
where k is a proportionality constant.
Conclusion
Thus, the relation between energy E, mass m, frequency n, and amplitude a is:
E=k⋅m⋅n2⋅a2
Energy E can be expressed in terms of force and displacement. The dimensional formula for force is given by:
Force=mass×acceleration=m⋅(lengthtime2)=m⋅LT2
Thus, the dimensions of force are:
(F)=MLT−2
Energy is defined as force multiplied by displacement:
E=Force×Displacement=F⋅L
So, the dimensions of energy are:
(E)=(F)⋅(L)=MLT−2⋅L=ML2T−2
We assume that energy E can be expressed as:
E∝manbac
where a, b, and c are the powers to which mass, frequency, and amplitude are raised, respectively.
- The dimension of mass m is:
(m)=M
- The frequency n is the reciprocal of time, so its dimension is:
(n)=T−1
- The amplitude a is a length, so its dimension is:
(a)=L
Substituting the dimensions into the expression for energy gives:
ML2T−2=(Ma)⋅(T−b)⋅(Lc)
This can be rewritten as:
Ma⋅Lc⋅T−b
Now, we equate the coefficients of M, L, and T from both sides:
1. For mass M:
a=1
2. For length L:
c=2
3. For time T:
−b=−2⟹b=2
From the values of a, b, and c, we can write the relation for energy:
E∝m1n2a2
or simply:
E=k⋅m⋅n2⋅a2
where k is a proportionality constant.
Thus, the relation between energy E, mass m, frequency n, and amplitude a is:
E=k⋅m⋅n2⋅a2
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Linked Comprehension
Explore 3 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Archives - Subjective
Explore 4 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Single Correct
Explore 93 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A : If displacement y of a particle executing simple harmonic motion depends upon amplitude a angular frequency ω and time t then the relation y=asinωt cannot be dimensionally achieved.
R : An equation cannot be achieved by dimensional analysis, if it contains dimensionless expressions.
View SolutionA body is vibrating in simple harmonic motion with an amplitude of 0.06 m and frequency of 15 Hz . The velocity and acceleration of body is
View Solution
Knowledge Check
A simple harmonic oscillator has a frequency of 2.5 Hz and an amplitude of 0.05m. What is the period of the oscillations?
A0.4sB0.2sC8sD20sFrequency of variation of kinetic energy of a simple harmonic motion of frequency n is
A2nBnCn2D3nConsider the following statements. The total energy of a particles executing simple harmonic motion depends on its
1. amplitude
2. Period
3. displacement of these :A1 and 2 are correctB2 and 3 are correctC1 and 3 are correctD1, 2 and 3 are correct
A particle executing of a simple harmonic motion covers a distance equal to half its amplitude in on e second . Then the time period of the simple harmonic motion is
View SolutionIf a body is executing simple harmonic motion and its current displacement is √3/2 times the amplitude from its mean position , then the ratio between potential energy and kinetic energy is
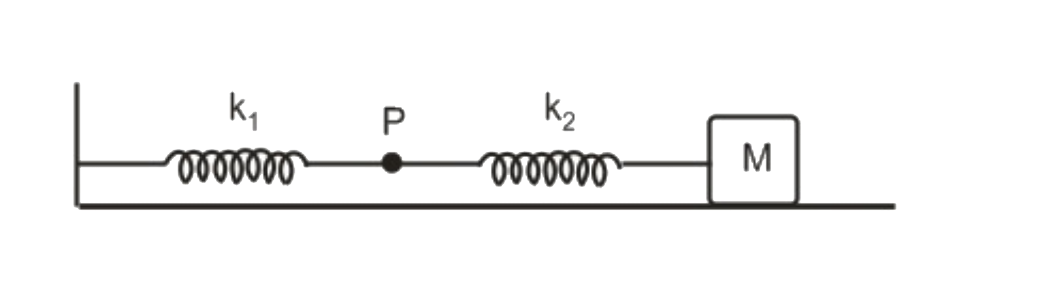
View SolutionThe mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is
View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View Solution