The equivalent capacitance between A and B is (in μF)

A
25
B
8425
C
1
D
2584
Text Solution
The correct Answer is:C

Starting from the right end of the network, three 3μF capacitors are connected in series. The equivalent capacitance of these three capacitors is
1CS=13+13+13⇒CS=1μF
Cs and 2μF are in parallel. The equivalent capacitance of these two capacitors is
CP=CS+2μf=1μF+2μF=3μF
Proceeding in this way, finally three 3μF are in series. Therefore, the equivalent capacitance between A and B is
1CAB=13+13+13⇒CAB=1μF
|
Topper's Solved these Questions
- ELECTROSTATICSBook:MTG GUIDEChapter:ELECTROSTATICSExercise:NEET ITALS
Explore 1 Video
- ELECTROSTATICSBook:MTG GUIDEChapter:ELECTROSTATICSExercise:NEET VITALS
Explore 18 Videos
- ELECTROSTATICSBook:MTG GUIDEChapter:ELECTROSTATICSExercise:AIPMT/NEET (MCQ.s)
Explore 34 Videos
- ELECTRONIC DEVICESBook:MTG GUIDEChapter:ELECTRONIC DEVICESExercise:AIPMT/NEET (MCQs)
Explore 42 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBook:MTG GUIDEChapter:MAGNETIC EFFECTS OF CURRENT AND MAGNETISMExercise:AIPMT/NEET (MCQs)
Explore 48 Videos
Similar Questions
Knowledge Check
Find equivalent capacitance between A and B
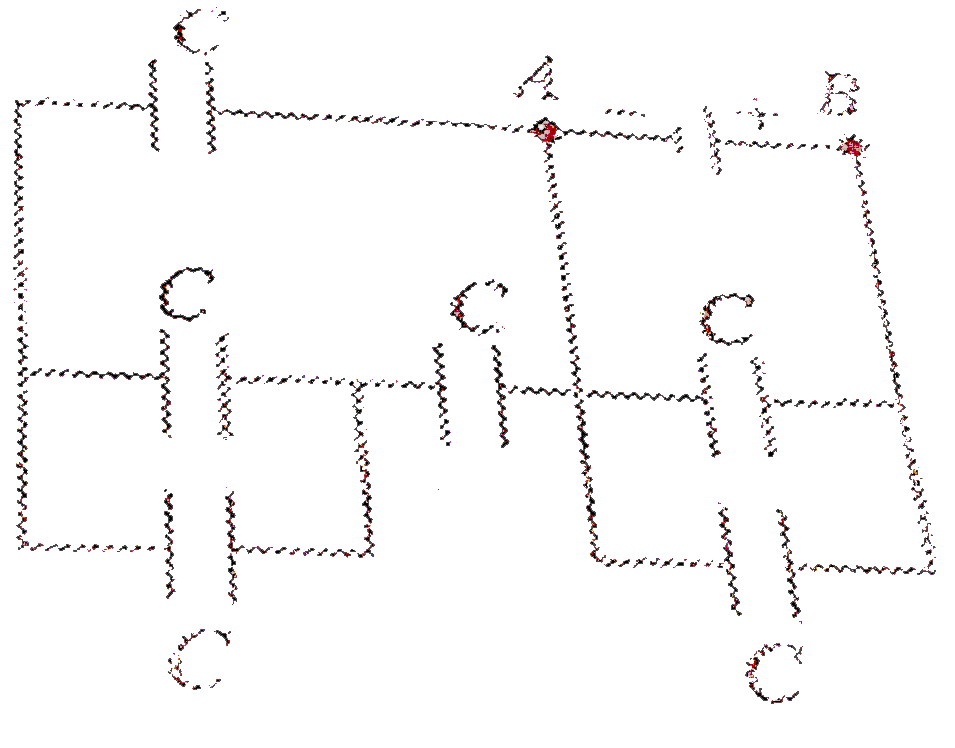 A6CB5CC3CD2C
A6CB5CC3CD2CFind equivalent capacitance between A & B
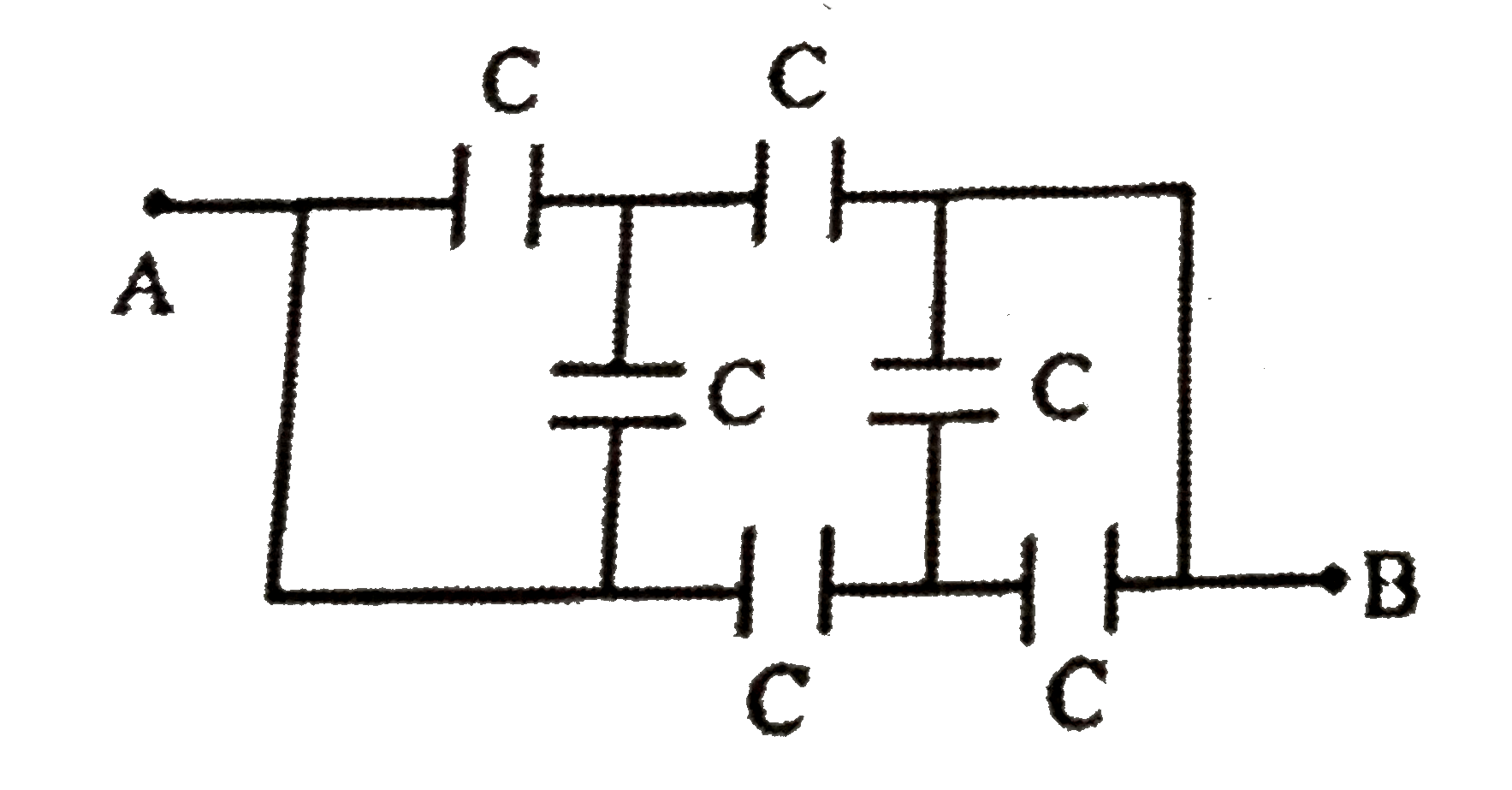 AC4B3G4C3G2D4G3
AC4B3G4C3G2D4G3The equivalent capacitance between point A and B is
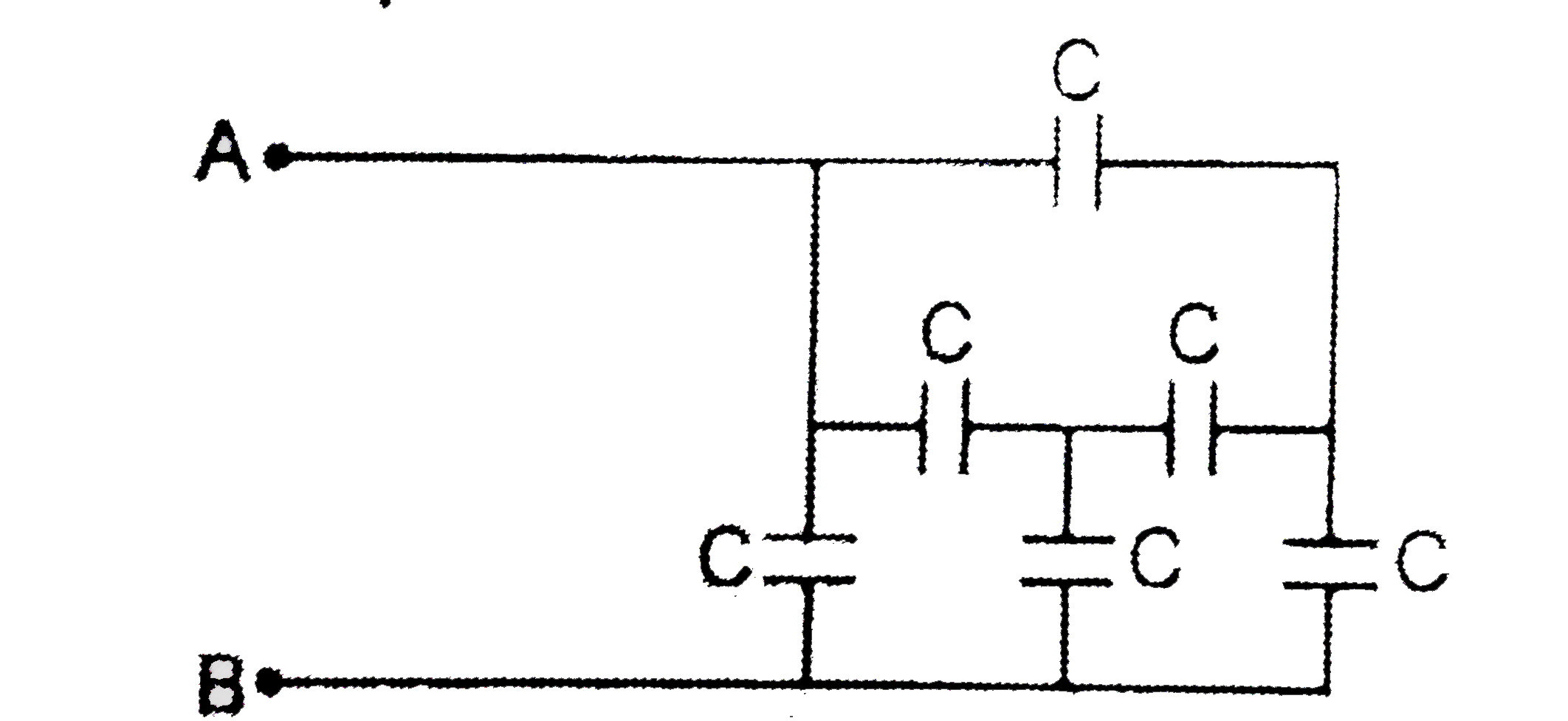 AC/4BC/2CCD2C
AC/4BC/2CCD2C
Find equivalent capacitance between A and B.
View SolutionThe equivalent capacitance between point A and B is
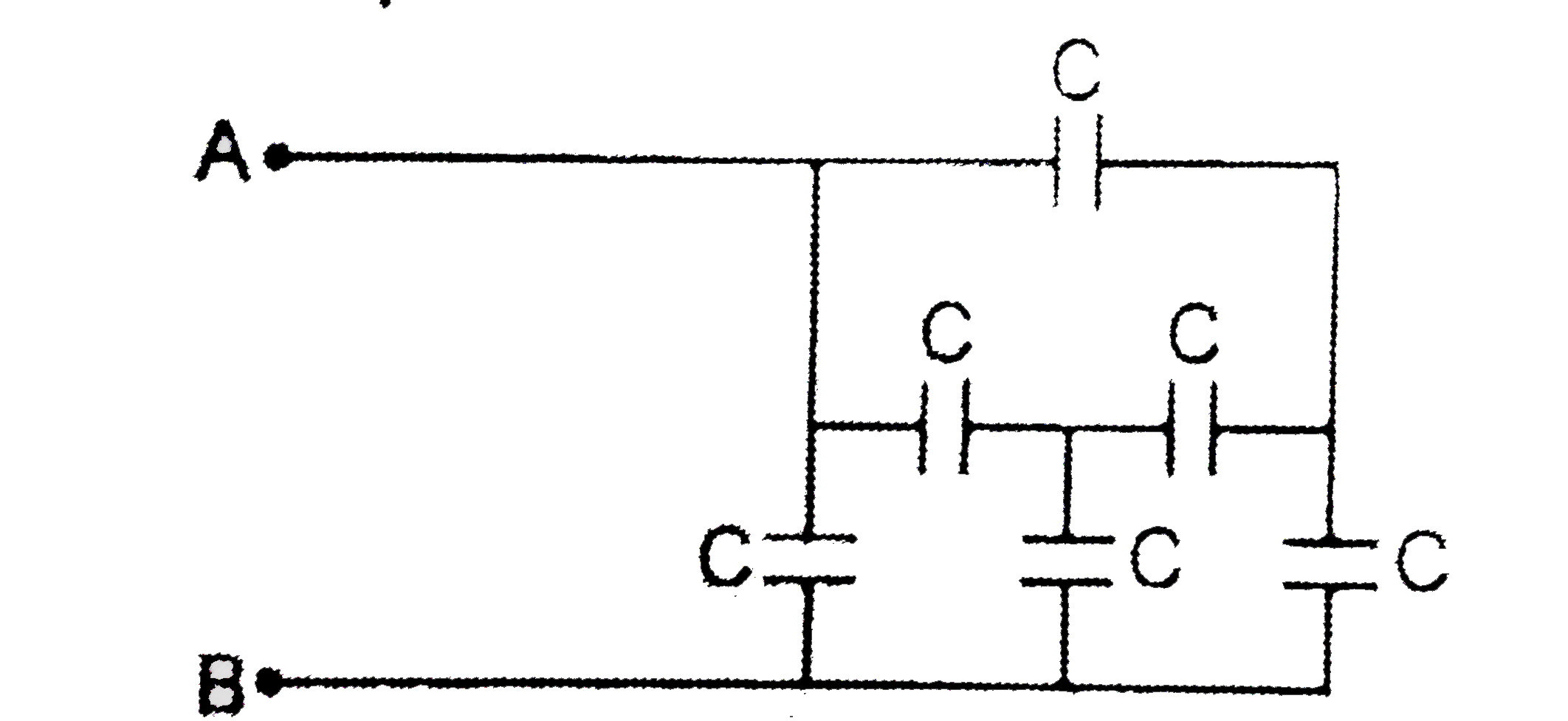
View SolutionThe equivalent capacitance between points A and B is

View SolutionFind the equivalent capacitance between A and B

View SolutionFind the equivalent capacitance between A and B

View Solution
