The faintest sound the human ear can detect at a frequency of 1000 Hz correspond to an intensity of about 1.00×10−12Wm2, which is called threshold of hearing. The loudest sounds the ear can tolerate at this frequency correspond to an intensity of about 1.00Wm2, the threshold of pain. Detemine the pressure amplitude and displacement amplitude associated with these two limits. Take speed of sound=342ms and density of air=1.20kgm3
Think about the quietest environment you have ever experienced. It is likely that the intensity of sound in even this quietest environment is higher than the threshold of hearing. Because we are given intesities and asked to calculate pressure and displacement amplitudes, this problem requires the concepts discussed in this section.
To find the pressure amplitude at the threshold of hearing,
tr∈∠Pmax=√2ρvI
=√2(1.20kgm3)(342ms)(1.00×10−12Wm2)
=2.87×10−5Wm2
Calculate the corresponding displacement amplitude using
Smax=△Pmaxρvω=2.87×10−5Nm2(1.20kgm3)(342ms)(2π×1000Hz)
=1.11×10−11m
In a similar manner, one finds that the loudest sounds the human ear can tolerate correspond to a pressure amplitude of 28.7Nm2 and a displacement amplitude equal to 1.11×10−5m.
Because atmospheric pressure is about 105Nm2, the result for the pressure amplitude tells us that the ear is sensitive to pressure fluctuations as small as 3 parts in 1010. The displacement amplitude is also a remarkably small number. If we compare this result for Smax to the size of an atom (about 10−10m), we see that the ear is an extremely sensitive detector of sound waves.
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Examples
56 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Exercise 6.1
56 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
The sound level at a distance of 3.00 m from a source is 120 dB. At what distance will the sound level be (a) 100 dB and (b) 10.0 dB?
View SolutionDo displacement particle velocity and pressure variation in a longitudinal wave vary with the same phase?
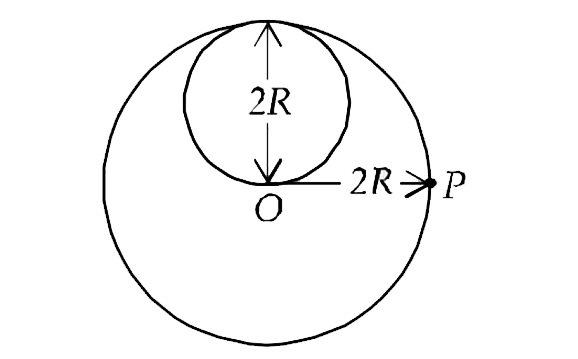
View SolutionA lamina is made by removing a small disc of diameter 2R from a bigger disc of uniform mass density and radius 2R, as shown in the figure. The moment of inertia of this lamina about axes passing though O and P is IOandIP respectively. Both these axes are perpendicular to the plane of the lamina. The ratio IPIO ot the nearest integer is
View SolutionA string of length L, fixed at its both ends is vibrating in its 1st overtone mode. Consider two elements of the string of the same small length at positions l1=0.2Landl2=0.45L from one end.
If K1andK2 are their respective maximum kinetic energies,then
View SolutionFor a person with normal hearing, the faintest sound that can be at a frequency of 400Hz has pressure amplitude of about 6.0×10−5 Pa . Calculate the corresponding intensity in W/m2 . Take speed of sound in air as 344m/s and density of air 1.2kg/m3 .
View SolutionFor a person with normal hearing, the faintest sound that can be heard at a frequency of 400 Hz has a pressure amplitude of about 6.0 xx 10^(-5) Pa . Calculate the corresponding intensity and sound intensity lavel at 20^(@) C . (Assume upsilon = 330 m//s and rho _(air) = 1.29 kg //m^(3) ).
View SolutionThe faintest sound that can be heard has a pressure ampulitude of about 2×10−5N/m2 and the loudest that can be heard without pain has a pressure ampulited of about 28N/m2. Dentermine in each (a) the intensity of the sound both in w/m2 and in dB and (b) the ampulited of the oscillations if the frequency is 500HZ. Assume an air density of 1.29kg/m3 and a velocity of sound is 345m/s.
View SolutionThe faintest sound the human ear can detect at a frequency of 1000 Hz correspond to an intensity of about 1.00×10−12Wm2, which is called threshold of hearing. The loudest sounds the ear can tolerate at this frequency correspond to an intensity of about 1.00Wm2, the threshold of pain. Detemine the pressure amplitude and displacement amplitude associated with these two limits. Take speed of sound=342ms and density of air=1.20kgm3
View SolutionThe minimum intensity of audibility of sound is 10^(-12) W//m^(2) s and density of air = 1.293 kg//m^(3) . If the frequency of sound in 1000 Hz , then the corresponding amplitude the vibration of the air particles is [ Take velocity of sound = 332 m//s ]
View SolutionThe faintest sound the human ear can detect at a frequency of kHz (for which ear is most sensitive) corresponds to an intensity of about 10−12w/m2. Assuming the density of air ≅1.5kg/m3 and velocity of sound in air ≅300m/s, the pressure amplitude and displacement amplitude of the sound will be rspectively ____N/m2 and ____m.
View SolutionThe maximum pressure variation that the human ear can tolerate in loud sound is about 30N/m2 . The corresponding maximum displacement for a sound wave in air having a frequency of 103Hz is
(Take velocity of sound in air as 300 m/s and density of air 1.5kg/m3)
View SolutionA blast given a sound of intensity 0.8 W//m^(2) at frequency 1kHz. If the denstiy of air is 1.3 kg//m^(3) and speed of sound in air is 330 m/s, then the amplitude of the sound wave is approximately
View SolutionMeasurement of sound waves show that the maximum pressure variations in the loudest sound that the ear can tolerate without pain are of the order of 30 Pa. Find the corresponding maximum displacement, if the frequency is 1000 Hz and v = 350 m//s
View SolutionThe faintest sound the human ear can detect at a frequency of 1kHz (for which the ear is most sensitive) corresponds to an intensity of about 10^(-12)W//m^2 (the so called threshold of hearing). Determine the pressure amplitude and maximum displacement associated with this sound assuming the density of air = 1.3kg//m^2 and velocity of sound in air = 332 m/s
View SolutionThe faintest sound the human ear can detect at a frequency of I kHz (fair which the ear is most sensitive) corresponds to an intensity of about 10^(-12)W//m^2 (the d threshold of hearing). Determine the pressure amplitude and maximum displacement associated with this sound assuming the density of air = 1.3kg//m^3 and velocity of soimtl in air= 332 m/s
View SolutionThe maximum pressure variation that the human ear can tolerate in loud sound is about 30 N/m2. Find the corresponding maximum displacement for a sound wave in air having a frequency of 103 Hz : (take velocity of sound in air as 300 m/s and density of air 1.5kg/m3)
View Solution
