The figure shows a spherical shell of mass M. The point a is not at the centre but away from the centre of the shell. If a particle of mass m is placed at A, then

it remains at rest
it experiences a net force towards the centre
it experiences a net force away from the centre
None of the above
The correct Answer is:A
E=0 inside a sheet. Therefore, gravitational force on m is zero.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 1 Subjective
19 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 Single Correct
22 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 1 Assertion And Reason
11 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
A thin spherical shell of total mass M and radius R is held fixed. There is a small hole in the shell. A mass m is released from rest a distance R from the hole along a line that passes through the hole and also through the centre of the shell. This mass subsequently moves under the gravitational force of the shell. How long does the mass take to travel from the hole to the point diametrically opposite.
View SolutionA point charge is kept at the centre of a metallic insulated spherical shell. Then
View Solution
Knowledge Check
A solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
A11GMmR2B14GMmR2CGMm2R2DGMmR2A particle of mass m is placed inside a spherical shell, away from its centre. The mass of the shell is M.
AThe particle will move towards the centre.BThe particle will move away from the centre, towards the nearest wall.CThe particle will move towards the centres if m<M, and away from the centre if m>M.DThe particle will remain stationary.Both question a and b refer to the sustem of charges as shown in the figure. A spherical shell of conducting material. A point charge +Q is place at the centre of the spherical shell and a total charge −q is placed on the shell. A Charge −q id distributed on the surfaces as
 .
.
(b) Assume that the elctrostatic potential is zero at an infinite distance from the spherical shell . The electrostatic potential at a distance R(a<R<b) from the centre of the shell is .A0BKQaCKQ−qRDKQ−qb(w≠reK=14πɛ0)
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

r<x<2r
View SolutionA point mass 'm' is placed inside a spherical shell of radius 'R' and mass 'M' at a distance from the centre of the shell. The gravitational force exerted by the shell on the point mass is -
View SolutionA point mass m is placed inside a spherical shell of radius R and mass M at a distance R2 form the centre of the shell. The gravitational force exerted by the shell on the point mass is
View SolutionA solid sphere of mass m radius r is placed inside a hollow thin spherical shell of mass M and radius 2r as shown in figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if
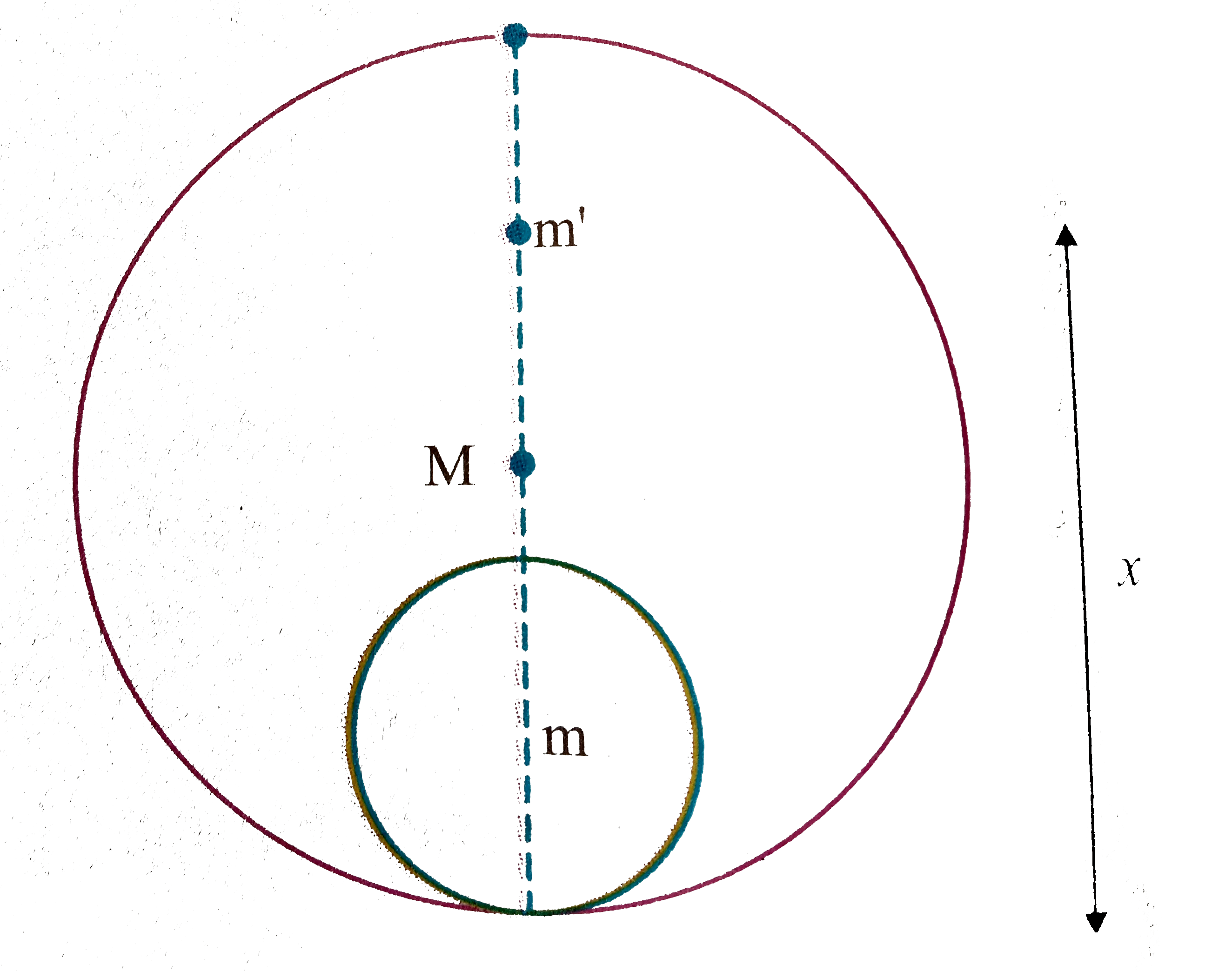
2r<x<2R
View SolutionA solid sphere of mass m radius r is placed inside a hollow thin spherical shell of mass M and radius 2r as shown in figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

x>2R
View Solution
