The figure shows a system of two concentric spheres of radii r1andr2 are kept at temperature T1andT2, respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to
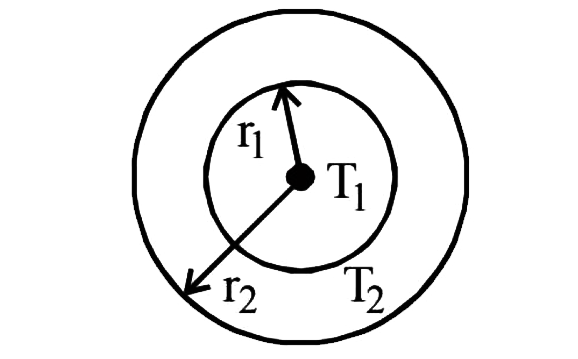
In(r2r1)
r2−r1r1r2
(r1−r2)
r1r2r2−r1
The correct Answer is:D
(d) 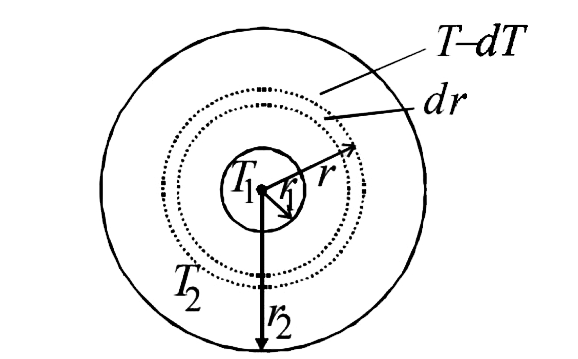
Consider a shell of thickness (dr) and of radius(r) and
the temperature of inner and outer surfaces of this shell
be T, (T−dT)
H=KA[(T−dT)−T]dr=−KAdTdr
H=−4πKr2dTdr⟨'A=4πr2)
Then, (H) int_(r_1)^(r_2) 1/(r^2) dr=-4piKint_(T_1)^(T_2) dT<br>H[1/(r_1)-1/(r_2)]=-4piK[T_2-T_1]<br>orH=(-4piKr_1r_2(T_2-T_1))/(r_2-r_1)
Topper's Solved these Questions
Similar Questions
Solve the foregoing problem for the case of two concentric spheres of radii R1 and R2 and temperatures T1 and T2.
View SolutionFig, shows a system of two concentric spheres of radii r1 andr2 and kept at temperature T1 and T2(T1>T2) respectively. Find the expression for radial rate of flow of heat through the substance.

View Solution
Knowledge Check
A system consists of two concentric spherical shells of radii a and b(b>a) maintained at temperature T1 and T2 respectively. The radial rate of flow of heat through substance between the two concentric spherical shells is proportional to
Ab - aBabb−aCloge(ba)Db−aabTwo spheres of the same material having radii r and 4r and temperature 2T0 and T0 respectively. The ratio of rate of radiation of energy by the sphere is
A1:1B1:2C2:1D3:1Two conducting spheres of radii r1 and r2 having charges Q1 and Q2 respectively are connected to each other. There is
Ano change in the energy of the systemBan increase in the energy of the systemCalways a decrease in the energy of the systemDa decrease in the energy of the system unless Q1r2=Q2r1
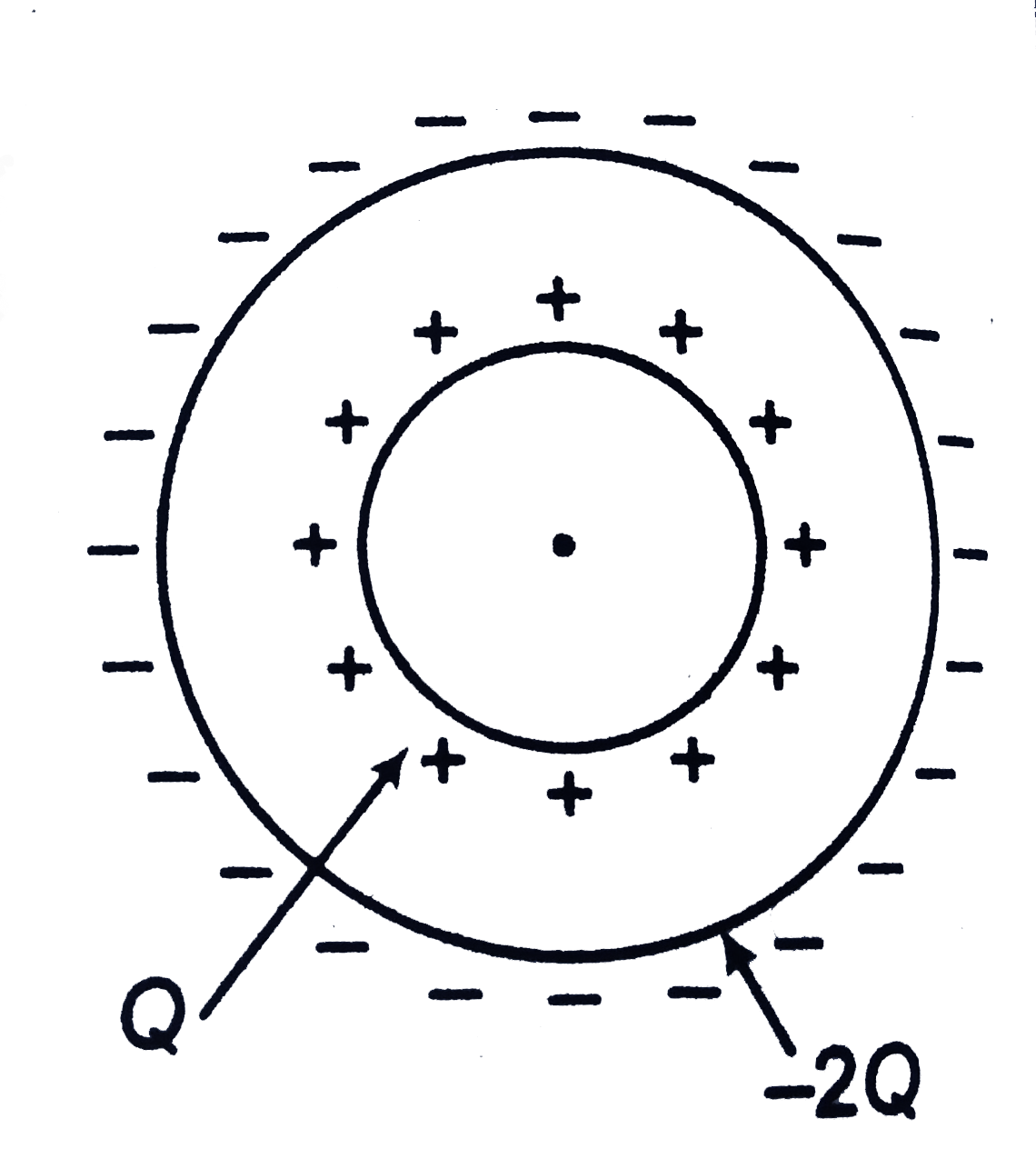
Two concentric conducting spheres of radii R and 2R are crrying charges Q and −2Q, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
View SolutionTwo spherical black bodies of radii R1 and R2 and with surface temperature T1 and T2 respectively radiate the same power. R1/R2 must be equal to
View SolutionThe capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
View SolutionThe figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is

View SolutionTwo conducting spheres of radii r1 and r2 are equally charged. The ratio of their potentral is-
View Solution
