The figure shows the variation of specific heat capacity (C ) of a solid as a function of temperature (T). The temperature is increased continuously from 0 to 500 K at a constant rate. Ignoring any volume change, the following statements(s) is/are correct to a reasonable approximation.
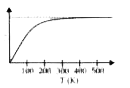
The rate at which heat is absorbed in the range 0-100 K varies linearly with temperature T
Heat absorbed in increasing the temperature from 0-100 K is less than the heat required for increasing the temperature from 400-500 K
There is no change in the rate of heat absorption in the range 400-500 K
The rate of heat absorption increases in the range 200-300 K
The correct Answer is:B, C, D
According to definition of specific heat capacity,
C=ΔQmΔTorΔQ=mCΔT
∴ΔQΔt=mCΔTΔt
Rate of heat absorbed = R=ΔQΔt
∴R∝C
(a) In 0-100 K, C increases with T but not linearly. So R increases but not linearly.
(b) As ΔQ=mCΔT
∴Q=m∫CΔT=m area under C-T curve
From the graph it is clear that area under C-T is more in 400-500 K than in 0-100 K.
Therefore, heat absorbed in 0-100 K is less than in 400 - 500 K.
(c ) In 400-500 K, C remains constant, so there is no change in R.
(d) In 200-300 K, C increases so R increases.

Topper's Solved these Questions
- KINETIC THEORY OF GASES BOOK - MTG-WBJEECHAPTER - KINETIC THEORY OF GASES EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (MCQ)
7 Videos
- KINEMATICS BOOK - MTG-WBJEECHAPTER - KINEMATICS EXERCISE - WB JEE Previous Years Questions (CATEGORY 3 : One or More than One Option Correct Type (2 Marks) )
1 Videos
- LAWS OF MOTION BOOK - MTG-WBJEECHAPTER - LAWS OF MOTION EXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))
2 Videos
Similar Questions
The figure below shows the variation of specific heat capacity (C) of a solid as a function of temperature (T). The temperature is increased continuously form 0 to 500K at a constant rate. Ignoring any volume change, the following statement (s) is (are) correct to a reasonable approximation.
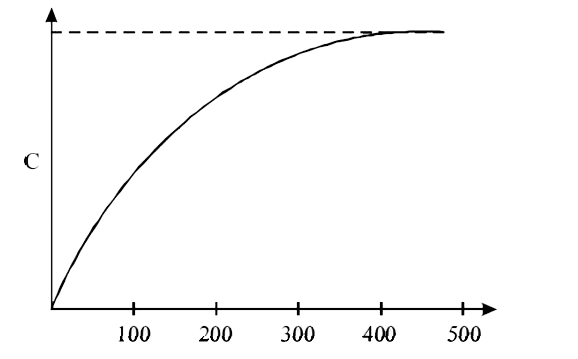
View SolutionThe figure below shows the variation of specific heat capacity (C) of a solid as a function of temperature (T). The temperature is increased continuously form 0 to 500K at a constant rate. Ignoring any volume change, the following statement (s) is (are) correct to a reasonable approximation.

View Solution
Knowledge Check
The figure below shows the variation of specific heat capacity (C) of a solid as a function of temperature (T). The temperature is increased continuousely form 0 to 500K at a constant rate. Ignorign any volume change, the following statement (s) is (are) correct to a reasonable approximation.
 AThe rate at which heat is absorbed in the range 0-100K varies linearly with temperature T.BHeat absorbed in increasing the temperature from 0-100K is less than the heat required for increasing the temperature from 400-500K.CThere is no change in the rate of heat absorption in the range 400-500K.DThe rate of heat absorption increases in the range 200-300K.
AThe rate at which heat is absorbed in the range 0-100K varies linearly with temperature T.BHeat absorbed in increasing the temperature from 0-100K is less than the heat required for increasing the temperature from 400-500K.CThere is no change in the rate of heat absorption in the range 400-500K.DThe rate of heat absorption increases in the range 200-300K.Plots showing the variation of the rate constant (k) with temperature (T) are given below. The plot that follows the Arrhenius equation is
A B
B C
C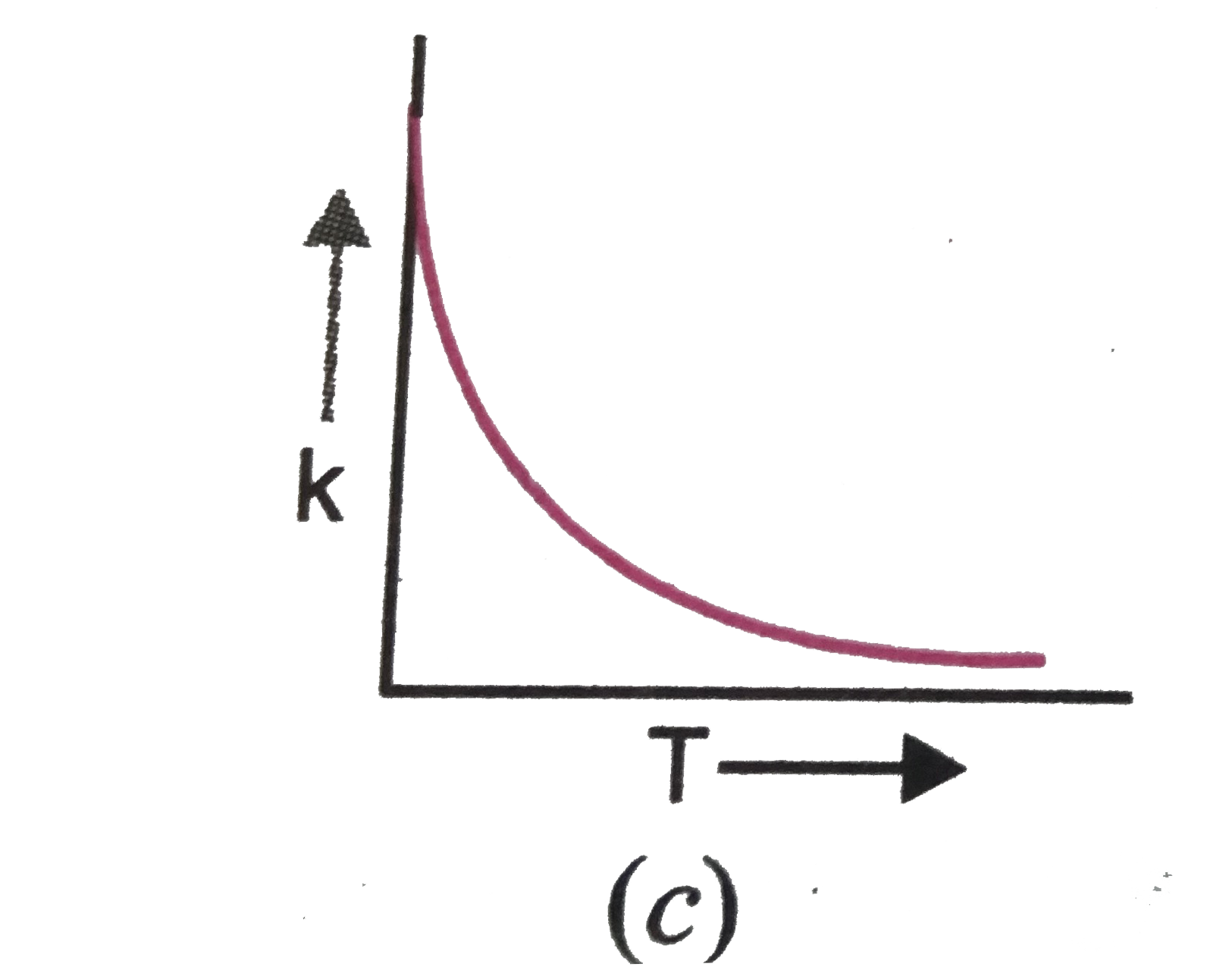 D
D
Plots showing the variation of the rate constant (k) with temperature (T) are given below. The plot that follows Arrhenius equations is
A B
B C
C D
D
The figure below shows the variation of specific heat capacity (C) of a solid as a function of temperature (T). The temperature is increased continuously form 0 to 500K at a constant rate. Ignoring any volume change, the following statement (s) is (are) correct to a reasonable approximation.

View SolutionThe temperature change versus heat supplied curve is given for 1 kg of a solid block. Then which of the following statement(s) is/are correct:

View SolutionPlots showing the variation of the rate constant (k) with temperature (T) are given below. The plot that follows the Arrhenius equation is
View SolutionPlots showing the variation of the rate constant (k) with temperature (T) are given below. The plot that follows the Arrhenius equation is
View SolutionPlots showing the variation of the rate constant (k) with temperature (T) are given below. The plot that follows the Arrhenius equation is
View Solution
