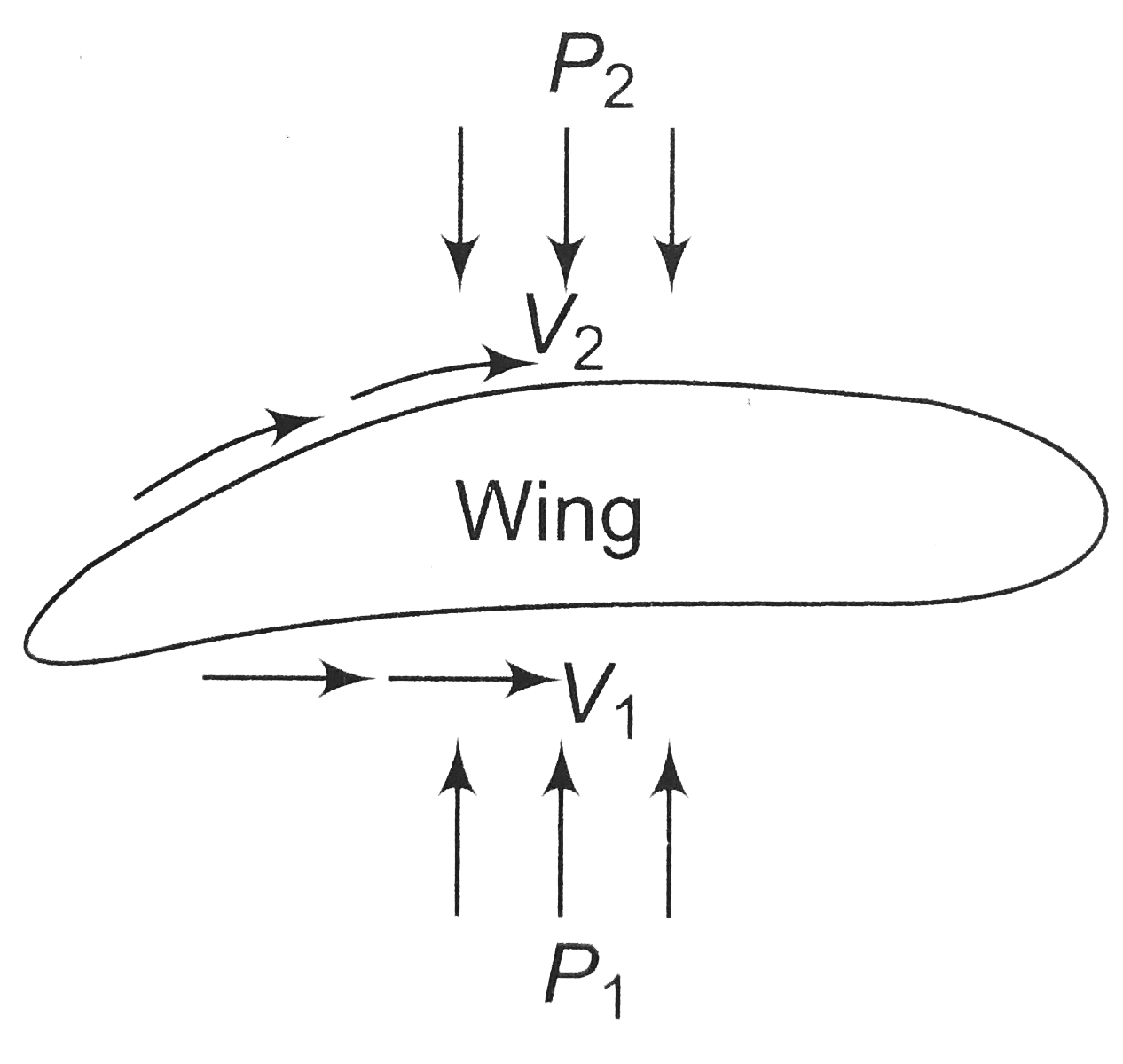
The flow speeds of air on the lower and upper surfaces of the wing ofan aeroplane are v and $\sqrt{2} v$ respectively. A is the area of the wing and $ρ$ is the density of th e surrounding air. What is the force of the dynamic lift on the wing ?

A

$\frac{1}{2} ρ v A$

B

$\frac{1}{2} ρ v^{2} A$

C

$ρ v^{2} A$

D

$\frac{ρ v^{2}}{2 A}$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:B

To find the force of dynamic lift on the wing of an airplane, we will use Bernoulli's principle, which relates the pressure difference between the upper and lower surfaces of the wing to the velocities of the air flowing over these surfaces.
1. Identify the given values:
- Speed of air on the lower surface, $v_{1} = v$
- Speed of air on the upper surface, $v_{2} = \sqrt{2} v$
- Area of the wing, $A$
- Density of air, $ρ$
2. Apply Bernoulli's equation:
Bernoulli's equation states that for incompressible flow, the sum of pressure energy, kinetic energy, and potential energy per unit volume is constant along a streamline. For our case, we can ignore the potential energy since the height difference is not given. Thus, we can write:
$P_{1} + \frac{1}{2} ρ v_{1}^{2} = P_{2} + \frac{1}{2} ρ v_{2}^{2}$
3. Rearranging Bernoulli's equation:
Rearranging the equation to find the pressure difference $P_{1} - P_{2}$ :
$P_{1} - P_{2} = \frac{1}{2} ρ v_{2}^{2} - \frac{1}{2} ρ v_{1}^{2}$
4. Substituting the values of $v_{1}$ and $v_{2}$ :
Substitute $v_{1} = v$ and $v_{2} = \sqrt{2} v$ :
$P_{1} - P_{2} = \frac{1}{2} ρ (\sqrt{2} v)^{2} - \frac{1}{2} ρ v^{2}$
Simplifying this gives:
$P_{1} - P_{2} = \frac{1}{2} ρ (2 v^{2}) - \frac{1}{2} ρ v^{2} = \frac{1}{2} ρ (2 v^{2} - v^{2}) = \frac{1}{2} ρ v^{2}$
5. Calculate the lift force:
The lift force $F_{L}$ is given by the pressure difference multiplied by the area of the wing:
$F_{L} = (P_{1} - P_{2}) \cdot A$
Substituting the pressure difference we found:
$F_{L} = (\frac{1}{2} ρ v^{2}) \cdot A$
6. Final expression for the lift force:
Thus, the force of dynamic lift on the wing is:
$F_{L} = \frac{1}{2} ρ v^{2} A$
Final Answer:
The force of dynamic lift on the wing is $F_{L} = \frac{1}{2} ρ v^{2} A$ .

|

Class 11 PHYSICS FRICTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

In a wind tunnel experiment the pressure on the upper and lower surfaces of the wings are $0.90 \times 10^{5} P a$ and $0.91 \times 10^{5} P a$ respectively. If the area of the wing is $40 m^{2}$ the net lifting force on the wing is
A $2 \times 10^{4} N$
B $4 \times 10^{4} N$
C $6 \times 10^{4} N$
D $8 \times 10^{4} N$
An aircraft is moving on a runway for its take off. The wind speed on the lower and upper surface of the wings are 'v' and $' \sqrt{2}' v$ . If the density of air is $ρ$ and surface area of the wing is A, the upward force exerted on thei wings will be
A $\sqrt{2} ρ v^{2} A$
B $\frac{1}{\sqrt{2}} ρ v^{2} A$
C $2 ρ v^{2} A$
D $\frac{1}{2} ρ v^{2} A$
In a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are $70 m s^{- 1}$ and $83 m s^{- 1}$ respectively. What is the lift on the wing, if its area is $2.5 m^{2}$ ? Take the density of air to be $1.3 k g m^{- 3}$
A $1513 N$
B1513 dines
C151.3 N
D151.3 dynes

MARVEL PUBLICATION-FRICTIONAL IN SOLIDS AND LIQUIDS -TEST YOUR GRASP

Home
Ask Doubt
Profile