The force acting on a particle moving parallel to the x-axis is F=2x+3x2. Calculate the work done in displacing the particle from x= 1 to x= 2.
F=2x+3x2
Work done =W=∫Fdx=∫21(2x+3x2)dx
=[2x22+6x33]21=[(22−12)+2(23−13)]
=17 units.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - ADDITIONAL SOLVED PROBLEMS138videos
DYNAMICS
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS20videos
DYNAMICS
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)9videos
DIMENSIONS
- BOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems30videos
FRICTION
Similar Questions
Force acting on a particle varies with x as shown in figure. Calculate the work done by the force as the particle moves from x = 0 to x = 6.0 m.
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The force acting on a bod moving parallel to the X-axis is F=3x+2x2. What is the work done in displacing the body from x=1 to x=2?
A656 unitsB256 unitsC556 unitsD356 units - Question 2 - Select One
A force F=Kx2 acts on a particle at an angle of 60° with the x–axis. the work done in displacing the particle from x1 to x2 will be –
Akx22Bk2(x22−x21)Ck6(x32−x31)Dk3(x32−x31) - Question 3 - Select One
A force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x=−a to x=+2a.
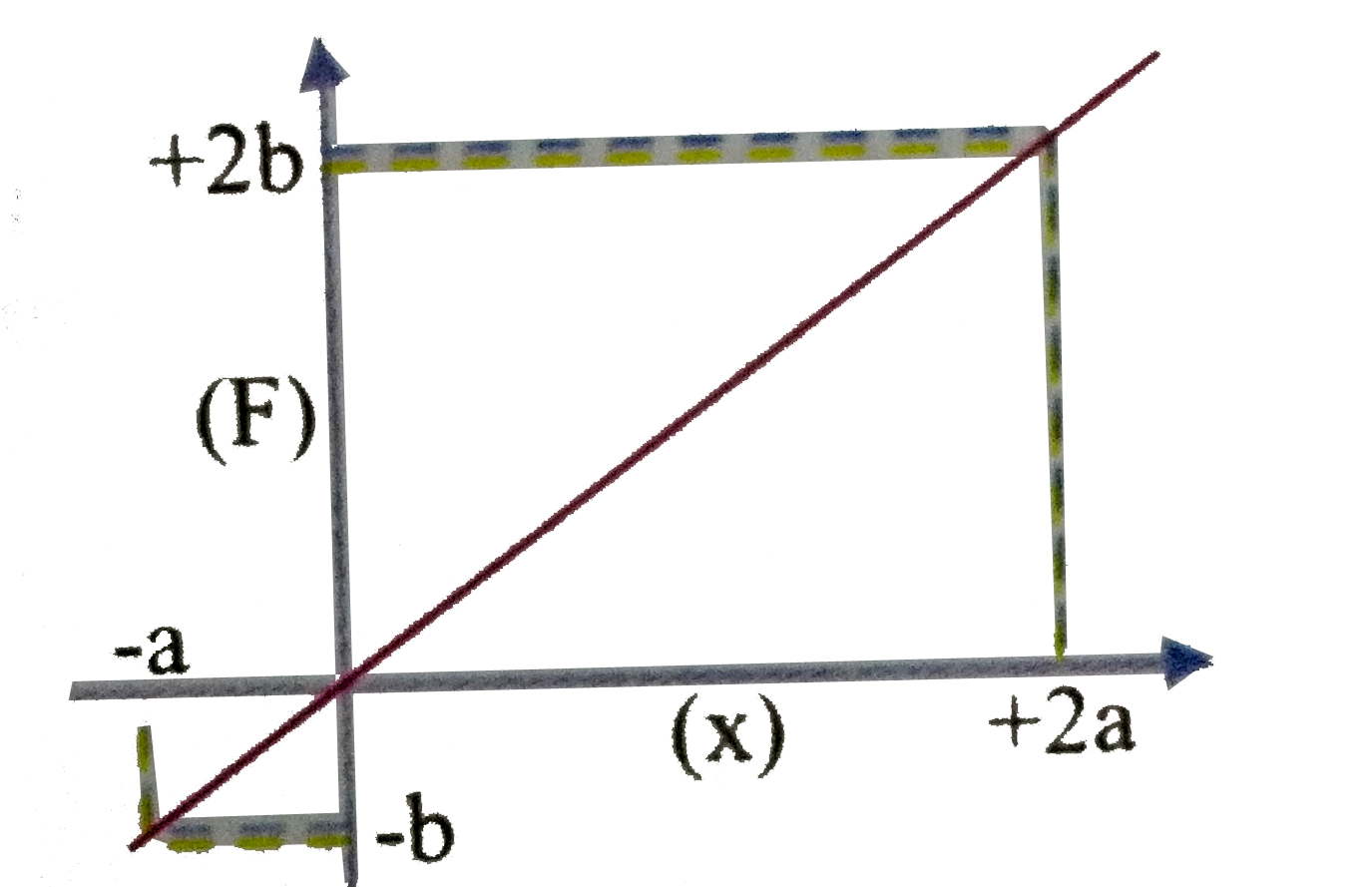 .A3ab2B4ab2C23abD24ab
.A3ab2B4ab2C23abD24ab
A force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from
 View Solution
View SolutionA force F = (10+0.25x) is acting on a particle moving along positive X direction . Calculate the work done by this force during a displacement from x = 1 m to x = 4 m .
View SolutionForce acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
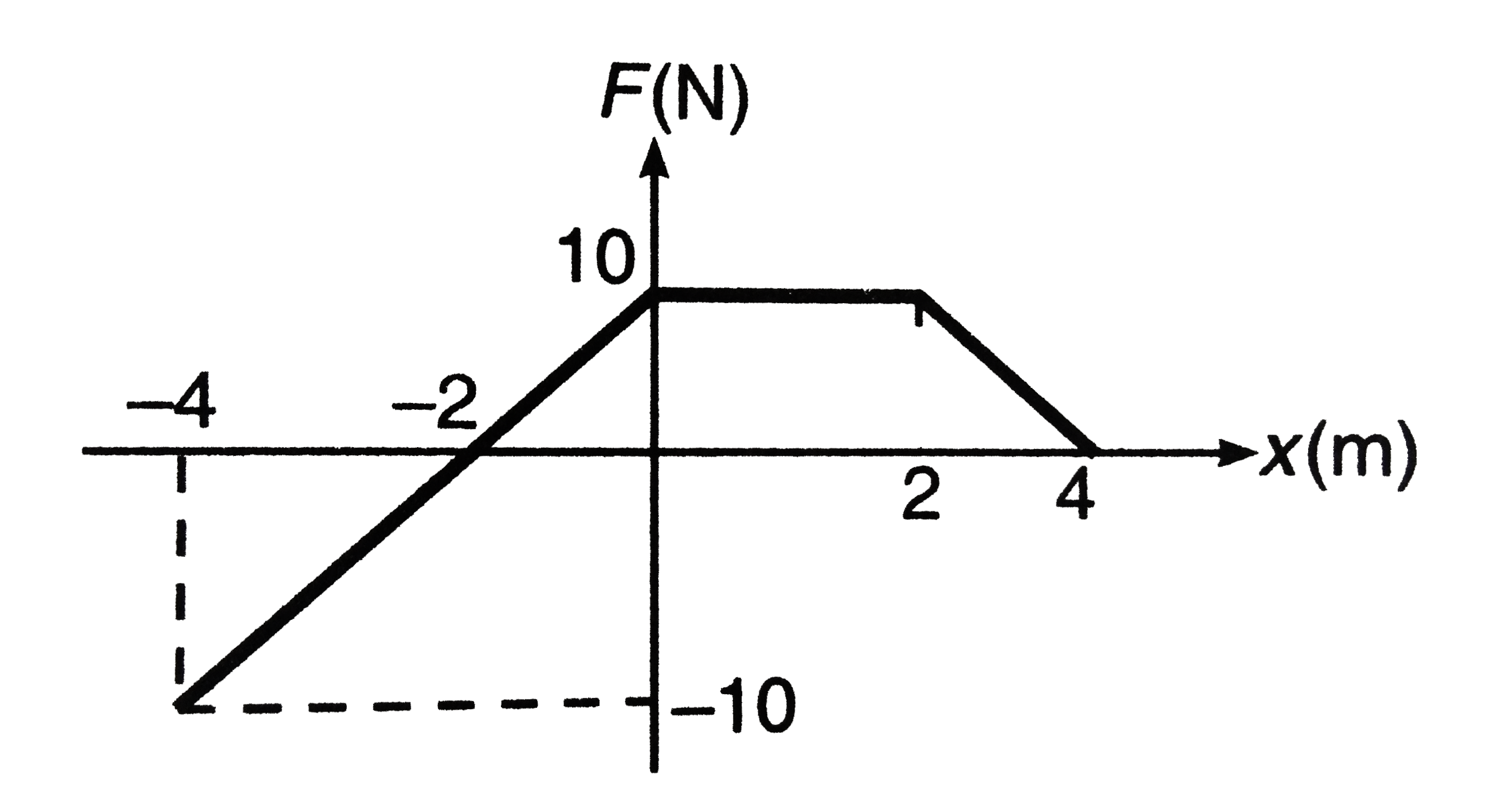 . View Solution
. View SolutionForce acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
 . View Solution
. View SolutionA force F = 0.5x + 10 acts on a particle. Here F is in newton and x is in metre. Calculate the work done by the force during the displacement of the particle from x = 0 to x = 2 metre.
View Solution
