The force constant of a weightless spring is 16Nm−1. A body of mass 1.0kg suspended from it is pulled down through 5cm and then released. The maximum energy of the sysytem (spring + body) will be
2×102J
4×102J
8×102J
16×102J
The correct Answer is:A
To solve the problem step by step, we will calculate the maximum energy of the system (spring + body) when the body is pulled down and released.
Step 1: Identify the Given Values
- Force constant of the spring, k=16N/m
- Mass of the body, m=1.0kg
- Displacement of the spring, x=5cm=0.05m (conversion from cm to m)
Step 2: Calculate the Maximum Potential Energy Stored in the Spring
The potential energy stored in a spring when it is compressed or stretched is given by the formula:
PE=12kx2
Substituting the values we have:
PE=12×16N/m×(0.05m)2
Step 3: Calculate x2
First, calculate (0.05)2:
(0.05)2=0.0025m2
Step 4: Substitute x2 into the Potential Energy Formula
Now substitute x2 back into the potential energy formula:
PE=12×16×0.0025
Step 5: Perform the Multiplication
Calculate 16×0.0025:
16×0.0025=0.04
Step 6: Calculate the Final Potential Energy
Now, calculate 12×0.04:
PE=12×0.04=0.02J
Conclusion
The maximum energy of the system (spring + body) will be:
Maximum Energy=0.02J=2×10−2J
---
- Force constant of the spring, k=16N/m
- Mass of the body, m=1.0kg
- Displacement of the spring, x=5cm=0.05m (conversion from cm to m)
The potential energy stored in a spring when it is compressed or stretched is given by the formula:
PE=12kx2
Substituting the values we have:
PE=12×16N/m×(0.05m)2
First, calculate (0.05)2:
(0.05)2=0.0025m2
Now substitute x2 back into the potential energy formula:
PE=12×16×0.0025
Calculate 16×0.0025:
16×0.0025=0.04
Now, calculate 12×0.04:
PE=12×0.04=0.02J
The maximum energy of the system (spring + body) will be:
Maximum Energy=0.02J=2×10−2J
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Mechanical Power
25 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Circular Motion In Vertical Plane
21 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Potential Energy, Conservative And Non-Conservative Forces
28 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
Force constant of a weightless spring is 16 N/m. A body of mass 1.0 kg suspended from it is pulled down through 5 cm from its mean position and the released. The maximum kinetic energy of the system (spring+body) will be (0.0x) J. Find value of x.
View SolutionA spring has a natural length of 50 cm and a force constant of 2.0×103 Nm−1. A body of mass 10 kg is suspended from it and the spring is stretched. If the body is pulled down to a length of 58 cm and released, it executes simple harmonic motion. The net force on the body when it is at its lowermost position of its oscillation is (10x) newton. Find value of x. (Take g=10m/s2)
View Solution
Knowledge Check
Force constant of a weightless spring is 16Nm−1. A body if mass 1 kg suspended from it is pulled down through 5 cm from its mean position and then released. The maximum kinetic energy of the body will be
A2×10−2JB4×10−2JC8×10−2JD16×10−2JMass suspended to a spring is pulled down by 2.5 cm and let go. The mass oscillates with an amplitude of
A2.5 cmB5 cmC7.5 cmD10 cmIf a body of mass 0.98 kg is made to oscillate on a spring of force constant 4.84 N/m the angular frequency of the body is
A1.22 rad/sB2.22 rad/sC3.22 rad/sD4.22 rad/s
Two bodies of masses 1 kg and 3 kg respectively are connected rigidly by a vertcal spring. The body of mass 3 kg rests on a smototh horizontal surface. The force constant of the spring is 484Nm−1. From the equilibrium position, the mass of 1 kg is displaced vertically through a distance of 0.02 m and then released. calculate (i) and frequency of oscillation of the mass of 1 kg (ii) the maximum velocity of this mass (iii) its oscillation energy and (iv) the reaction of the table on the mass of 3 kg, when mass 1 kg is having harmonic oscillations.
View SolutionA body of mass m is suspended from a massless spring of natural length l. It stretches the spring through a vertical distance y. The potential energy of the stretched spring is
View SolutionA spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring,pulled sideways to a distance of 2 cm and released . The speed of the mass when the spring is compressed by 1 cm is
View SolutionA body of mass 5 kg is suspended by a spring balance on an inclined plane as shown in figure. The spring balance measure
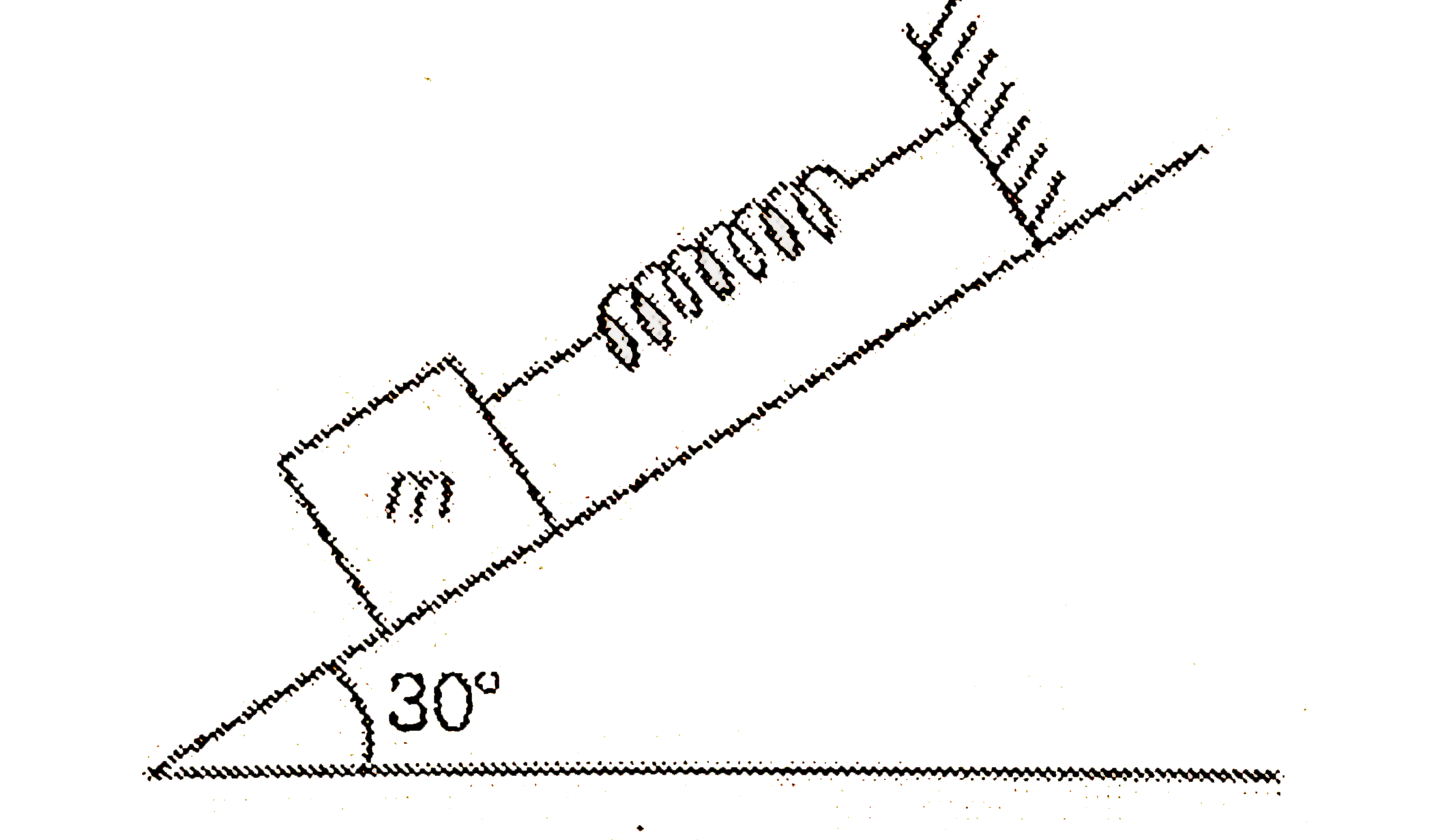
View SolutionA body of mass 5 kg is suspended by a spring balance on an inclined plane as shown in figure. The spring balance measure

View Solution
