The frequency and the intensity of a beam of light falling on the surface of a photoelectric material are increased by a factor of two. This will
increase the maximum kinetic energy, the photoelectrons, as well as photoelectric current by a factor of 2
increase the maximum kinetic energy of the photoelectrons and would increase the photoelectric current by a factor of 2
increase the maximum kinetic energy of the photoelectrons by a factor of 2 and will gave no effect on the magnitude of the photoelectric current produced
not produce any effect on the kinetic energy of the emitted electrins but will increase the photoelectric current by a factor of 2
The correct Answer is:B
To solve the problem, we will analyze the effects of increasing the frequency and intensity of light on the photoelectric effect, specifically focusing on the maximum kinetic energy of emitted electrons and the photoelectric current.
1. Understanding the Photoelectric Effect:
The photoelectric effect describes the emission of electrons from a material when it is exposed to light (photons). The maximum kinetic energy (K.E.) of the emitted electrons can be expressed using Einstein's photoelectric equation:
K.E.=Ephoton−ϕ
where Ephoton=hν (energy of the photon), h is Planck's constant, ν is the frequency of light, and ϕ is the work function of the material.
2. Initial Conditions:
Let the initial frequency of light be ν. The initial maximum kinetic energy of the emitted electrons is:
K.E.max=hν−ϕ
3. Increasing Frequency:
The problem states that the frequency of the light is increased by a factor of 2. Thus, the new frequency becomes:
ν′=2ν
The energy of the photon at this new frequency is:
E′photon=hν′=h(2ν)=2hν
The new maximum kinetic energy of the emitted electrons is:
K.E.′max=E′photon−ϕ=2hν−ϕ
4. Comparing Maximum Kinetic Energies:
We can express the new maximum kinetic energy in terms of the initial maximum kinetic energy:
K.E.′max=2hν−ϕ=2(K.E.max+ϕ)−ϕ=2K.E.max+ϕ
This shows that the new maximum kinetic energy is greater than twice the initial maximum kinetic energy because of the additional ϕ.
5. Increasing Intensity:
The intensity of light is also increased by a factor of 2. Intensity is directly proportional to the number of photons incident on the surface. Therefore, if the intensity is doubled, the number of photons is also doubled, which means the number of emitted electrons (assuming 100% quantum efficiency) will also double.
6. Conclusion:
- The maximum kinetic energy of the photoelectrons increases by more than a factor of 2 due to the increase in frequency.
- The photoelectric current, which is proportional to the number of emitted electrons, increases by a factor of 2 due to the increase in intensity.
Thus, the correct answer is that the maximum kinetic energy of the photoelectrons increases and the photoelectric current increases by a factor of 2.
Final Answer:
- The maximum kinetic energy of the photoelectrons increases by more than a factor of 2.
- The photoelectric current increases by a factor of 2.
The photoelectric effect describes the emission of electrons from a material when it is exposed to light (photons). The maximum kinetic energy (K.E.) of the emitted electrons can be expressed using Einstein's photoelectric equation:
K.E.=Ephoton−ϕ
where Ephoton=hν (energy of the photon), h is Planck's constant, ν is the frequency of light, and ϕ is the work function of the material.
Let the initial frequency of light be ν. The initial maximum kinetic energy of the emitted electrons is:
K.E.max=hν−ϕ
The problem states that the frequency of the light is increased by a factor of 2. Thus, the new frequency becomes:
ν′=2ν
The energy of the photon at this new frequency is:
E′photon=hν′=h(2ν)=2hν
The new maximum kinetic energy of the emitted electrons is:
K.E.′max=E′photon−ϕ=2hν−ϕ
We can express the new maximum kinetic energy in terms of the initial maximum kinetic energy:
K.E.′max=2hν−ϕ=2(K.E.max+ϕ)−ϕ=2K.E.max+ϕ
This shows that the new maximum kinetic energy is greater than twice the initial maximum kinetic energy because of the additional ϕ.
The intensity of light is also increased by a factor of 2. Intensity is directly proportional to the number of photons incident on the surface. Therefore, if the intensity is doubled, the number of photons is also doubled, which means the number of emitted electrons (assuming 100% quantum efficiency) will also double.
- The maximum kinetic energy of the photoelectrons increases by more than a factor of 2 due to the increase in frequency.
- The photoelectric current, which is proportional to the number of emitted electrons, increases by a factor of 2 due to the increase in intensity.
- The maximum kinetic energy of the photoelectrons increases by more than a factor of 2.
- The photoelectric current increases by a factor of 2.
Topper's Solved these Questions
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Multiple Correct
10 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Linked Comprehension
44 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Subjective
16 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
Similar Questions
Knowledge Check
Two waves of same frequency and intensity superimpose on each other in opposite phases. After the superposition the intensity and frequency of waves will.
A1. increaseB2. decreaseC3. remains constantD4. becomes zero
Ultraviolet light of wavelength 300nm and intensity 1.0Wm−2 falls on the surface of a photosensitive material. If one per cent of the incident photons produce photoelectrons, then the number of photoelectrons emitted per second from an area of 1.0 cm2 of the surface is nearly
View SolutionIntensity of light incident on a photo sensitive surface is doubled. Then
View SolutionIf λ0 is the threshold wavelength for photoelectric emission. λ wavelength of light falling on the surface on the surface of metal, and m mass of electron. Then de Broglie wavelength of emitted electron is :-
View SolutionThe ray of light that strikes or falls on a reflecting surface
View SolutionA : On increasing the intensity of light , the number of photoelectrons emitted is more . Also the kinetic energy of each photo increases but the photoelectric current is constant
R : Photoelectric current is independent of intensity but increases with increasing frequency incident radiation
View SolutionA light beam consists of two types of photons. In one type, each photon has the energy 2 eV and in another type, each photon has energy 3 eV. The light beam is incident on a photoelectric material of work function 1 eV. The maximum kinetic enregy of emitted photoelectron is
View SolutionThe following figure shows a graph for the stopping potential as a function of the frequency of incident light illuminating a metal surface. Find the photoelectric work function for this surface.
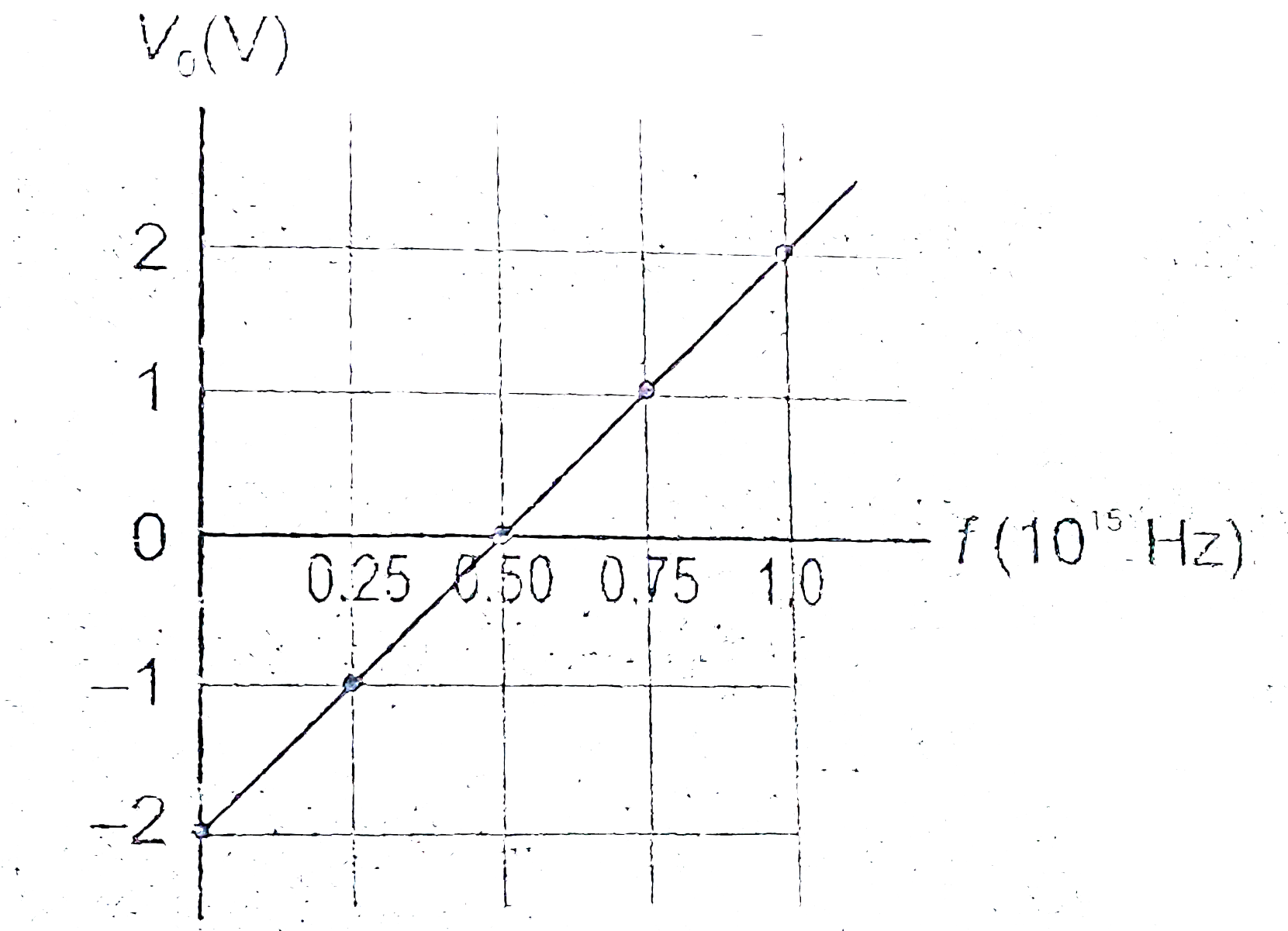
View Solution
