The frequency of an octave is 576Hz. Find the 5th note of major diatomic scale.
To find the 5th note of the major diatonic scale given that the frequency of an octave is 576 Hz, we can follow these steps:
Step 1: Understand the Major Diatonic Scale
The major diatonic scale consists of the following notes: A, B, C#, D, E, F#, G#. However, in this case, we are interested in the notes A, D, E, F, G, and the 5th note, which is G.
Step 2: Establish Relationships Between Frequencies
We know the following relationships for the frequencies of the notes in the major diatonic scale:
- Frequency of D = (9/8) × Frequency of A
- Frequency of E = (10/9) × Frequency of D
- Frequency of F = (16/15) × Frequency of E
- Frequency of G = (9/8) × Frequency of F
Step 3: Express Frequency of G in Terms of Frequency of A
We can express the frequency of G in terms of the frequency of A:
1. Frequency of D = (9/8) × Frequency of A
2. Frequency of E = (10/9) × Frequency of D = (10/9) × (9/8) × Frequency of A = (10/8) × Frequency of A = (5/4) × Frequency of A
3. Frequency of F = (16/15) × Frequency of E = (16/15) × (5/4) × Frequency of A = (16 × 5)/(15 × 4) × Frequency of A = (80/60) × Frequency of A = (4/3) × Frequency of A
4. Frequency of G = (9/8) × Frequency of F = (9/8) × (4/3) × Frequency of A = (36/24) × Frequency of A = (3/2) × Frequency of A
Step 4: Calculate the Frequency of G
Now, we can substitute the frequency of A with the given frequency of the octave, which is 576 Hz:
- Frequency of G = (3/2) × 576 Hz
Calculating this:
- Frequency of G = (3 × 576) / 2 = 1728 / 2 = 864 Hz
Final Answer
The frequency of the 5th note (G) of the major diatonic scale is 864 Hz.
---
The major diatonic scale consists of the following notes: A, B, C#, D, E, F#, G#. However, in this case, we are interested in the notes A, D, E, F, G, and the 5th note, which is G.
We know the following relationships for the frequencies of the notes in the major diatonic scale:
- Frequency of D = (9/8) × Frequency of A
- Frequency of E = (10/9) × Frequency of D
- Frequency of F = (16/15) × Frequency of E
- Frequency of G = (9/8) × Frequency of F
We can express the frequency of G in terms of the frequency of A:
1. Frequency of D = (9/8) × Frequency of A
2. Frequency of E = (10/9) × Frequency of D = (10/9) × (9/8) × Frequency of A = (10/8) × Frequency of A = (5/4) × Frequency of A
3. Frequency of F = (16/15) × Frequency of E = (16/15) × (5/4) × Frequency of A = (16 × 5)/(15 × 4) × Frequency of A = (80/60) × Frequency of A = (4/3) × Frequency of A
4. Frequency of G = (9/8) × Frequency of F = (9/8) × (4/3) × Frequency of A = (36/24) × Frequency of A = (3/2) × Frequency of A
Now, we can substitute the frequency of A with the given frequency of the octave, which is 576 Hz:
- Frequency of G = (3/2) × 576 Hz
- Frequency of G = (3 × 576) / 2 = 1728 / 2 = 864 Hz
The frequency of the 5th note (G) of the major diatonic scale is 864 Hz.
Topper's Solved these Questions
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Sound Waves
50 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Musical Sound
2 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Solved Examples
17 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS
79 Videos
Similar Questions
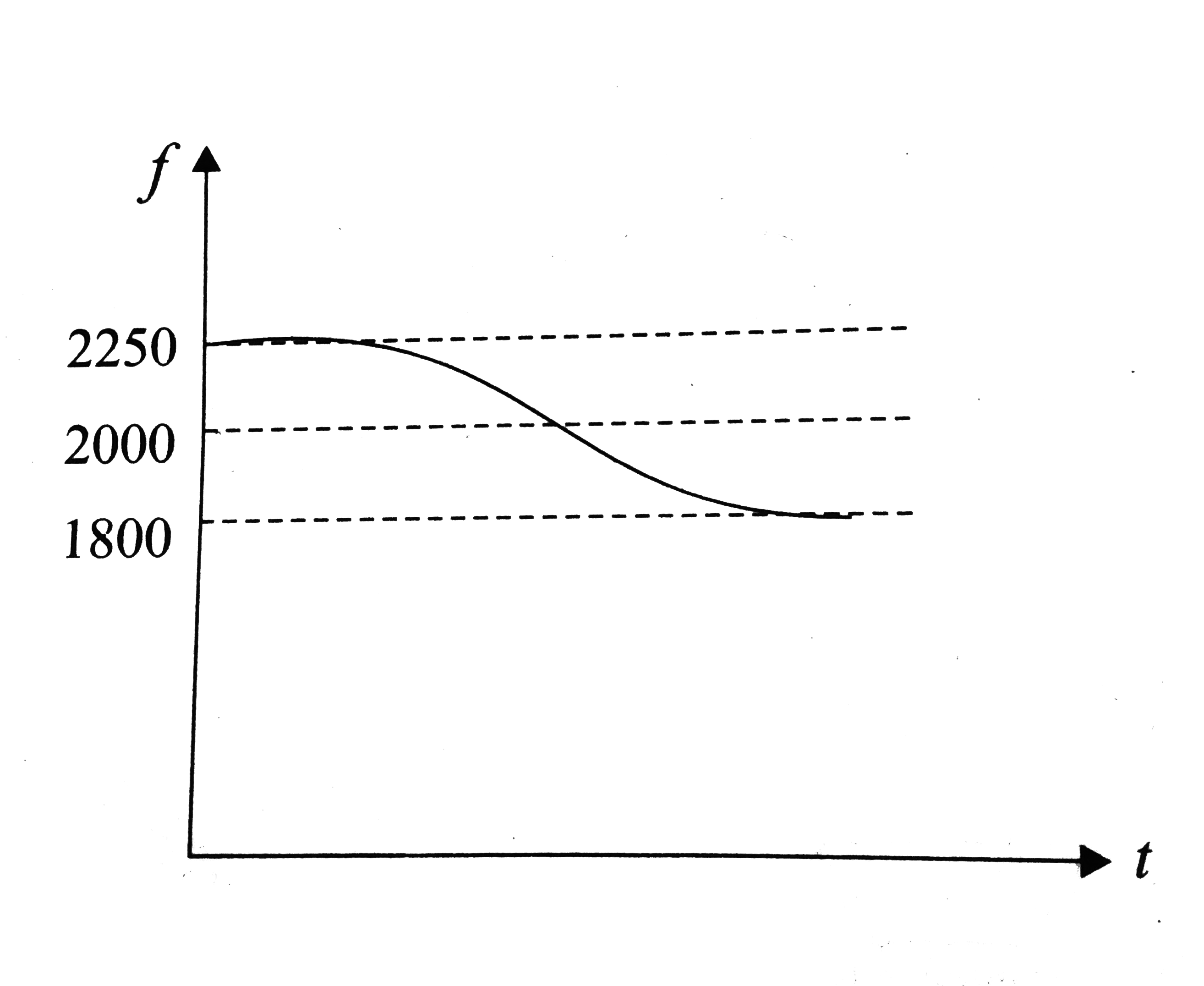
A statinary observer receives a sound of frequency 2000 Hz. The variation of apparent frequency and time is shown. Find the speed of source, if velocity of sound is 300ms
View SolutionThe frequency of the fundamental note of a tube closed at one end is 200 Hz. What will be the frequency of the fundamental note of a similar tube of the same length but open at both ends ?
View Solutionthe frequency of a sonometer wire is 100 Hz. When the weight producing th tensions are completely immersed in water the frequency becomes 80 Hz and on immersing the weight in a certain liquid the frequency becomes 60 Hz. The specific gravity of the liquid is
View SolutionThe frequeny of the fundamental note emitted from an organ pipe is 200 Hz. When sir is blown forcefully the frequency of the first overtone emitted is 600 Hz. Is the pipe open or closed ?
View SolutionThe mean of the following frequency distribution is 57.6 and the sum of the observations is 50. Find the missing frquencies f1andf2 :

View SolutionA road passes at some distance from a standing man. A truck is coming on the road with some acceleration. The truck driver blows a whistle of frequency 500Hz when the line joining the truck and the man makes an angle θ with the road. The man hears a note having a note having a frequency of 600Hz when the truck is closest to him. Also the speed of truck has get doubled during this time. Find the value of 'θ'.
View SolutionThe string of violin emits a note of 440 Hz at its correct tension. The string is bit taut and produces 4 beats per second with a tuning fork of frequency 440 Hz. Find the frequency of the note emitted by this taut string.
View SolutionThe frequencies of notes given by flute, guitar and trumpet are respectively 400 Hz, 200 Hz and 500 Hz. Which one of these has the highest pitch ?
View SolutionA middle C string on a piano has a fundamental frequency of 262Hz, and the A note has fundamental frequency of 440Hz. (a) Calculate the frequencies of the next two harmonics of the C string. (b) If the strings for the A and C notes are assumed to have the same mass per unit length and the same length, determine the ratio of tension in the two strings.
View SolutionThe 5th term of an A.P. is 11 and the 9th term is 7. Find the 16th term.
View Solution