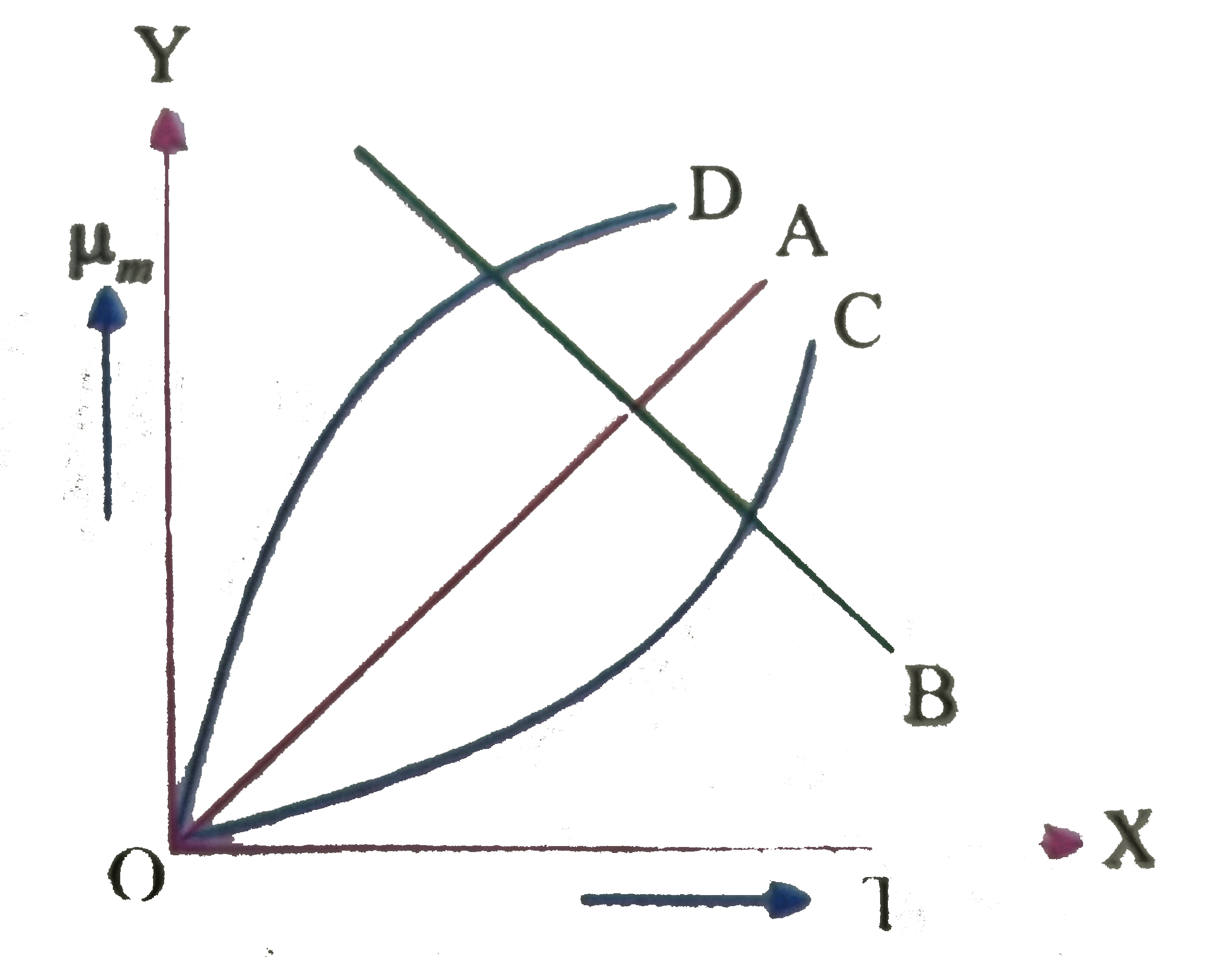
The frequency (vm) corresponding to which energy emitted by a black body is maximum may vary with temperature T of the body as shown in Which of the curves repersents correct variation ?
 .
.
curve D
curve C
curve B
curve A
The correct Answer is:C
λm∝1Tandv∝T
∴ The curve B represents the correct variation.
Topper's Solved these Questions
- KINETIC THEORY OF GASES ,THERMODYNAMICS AND RADIATIONBOOK - MARVEL PUBLICATIONCHAPTER - KINETIC THEORY OF GASES ,THERMODYNAMICS AND RADIATIONEXERCISE - TEST YOUR GRASP - 9
30 Videos
- INTERFERENCE AND DIFFRACTIONBOOK - MARVEL PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - TEST YOUR GRASP
20 Videos
- MAGNETIC EFFECTS OF ELECTRIC CURRENTBOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECTS OF ELECTRIC CURRENTEXERCISE - MCQ
195 Videos
Similar Questions
The shows a radiant energy spectrum graph for a black body at at temperature T
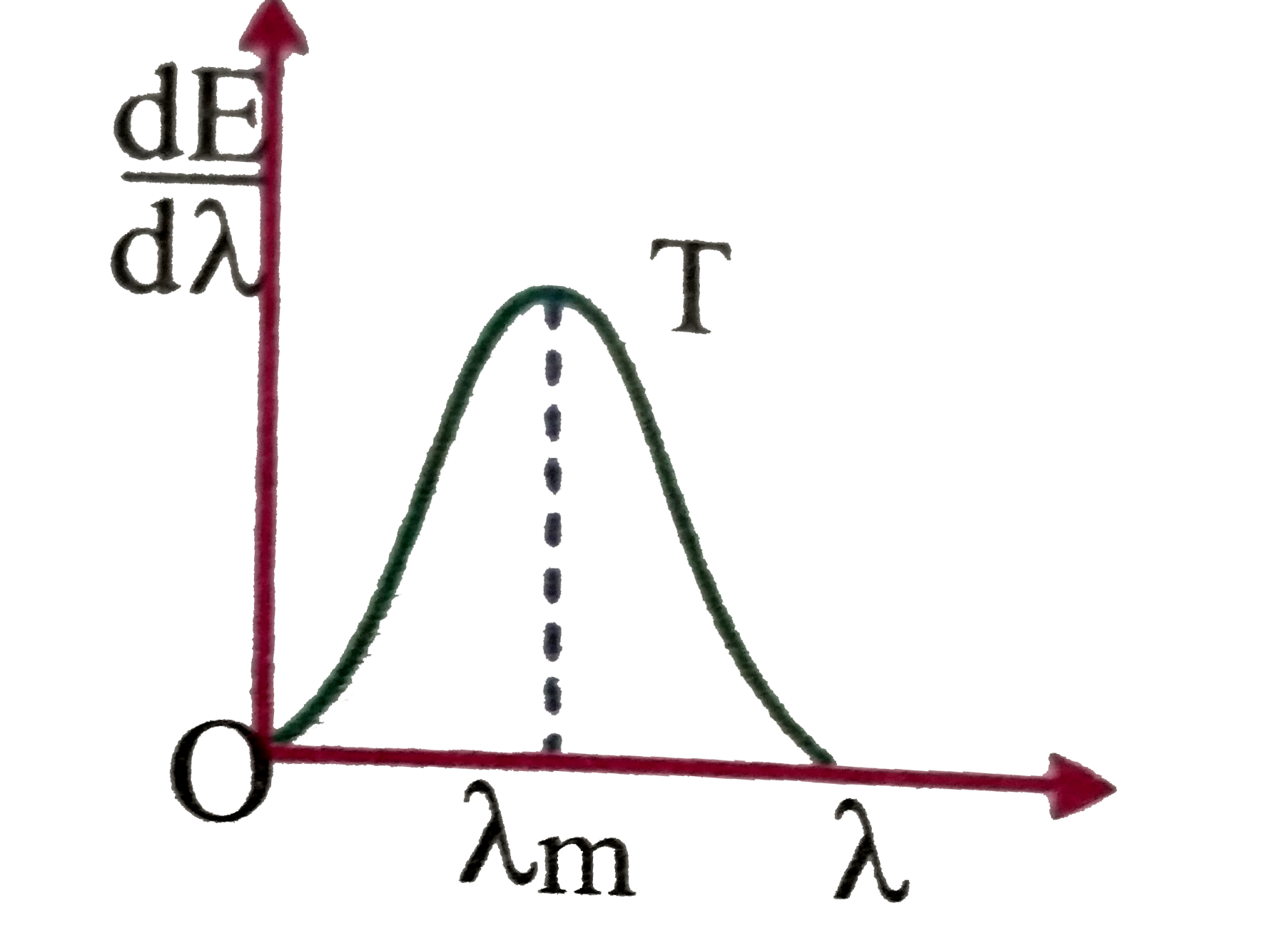
If the temperature of the body is raised to a higher temperature T then choose the correct statement (s).
View SolutionThe shows a radiant energy spectrum graph for a black body at at temperature T
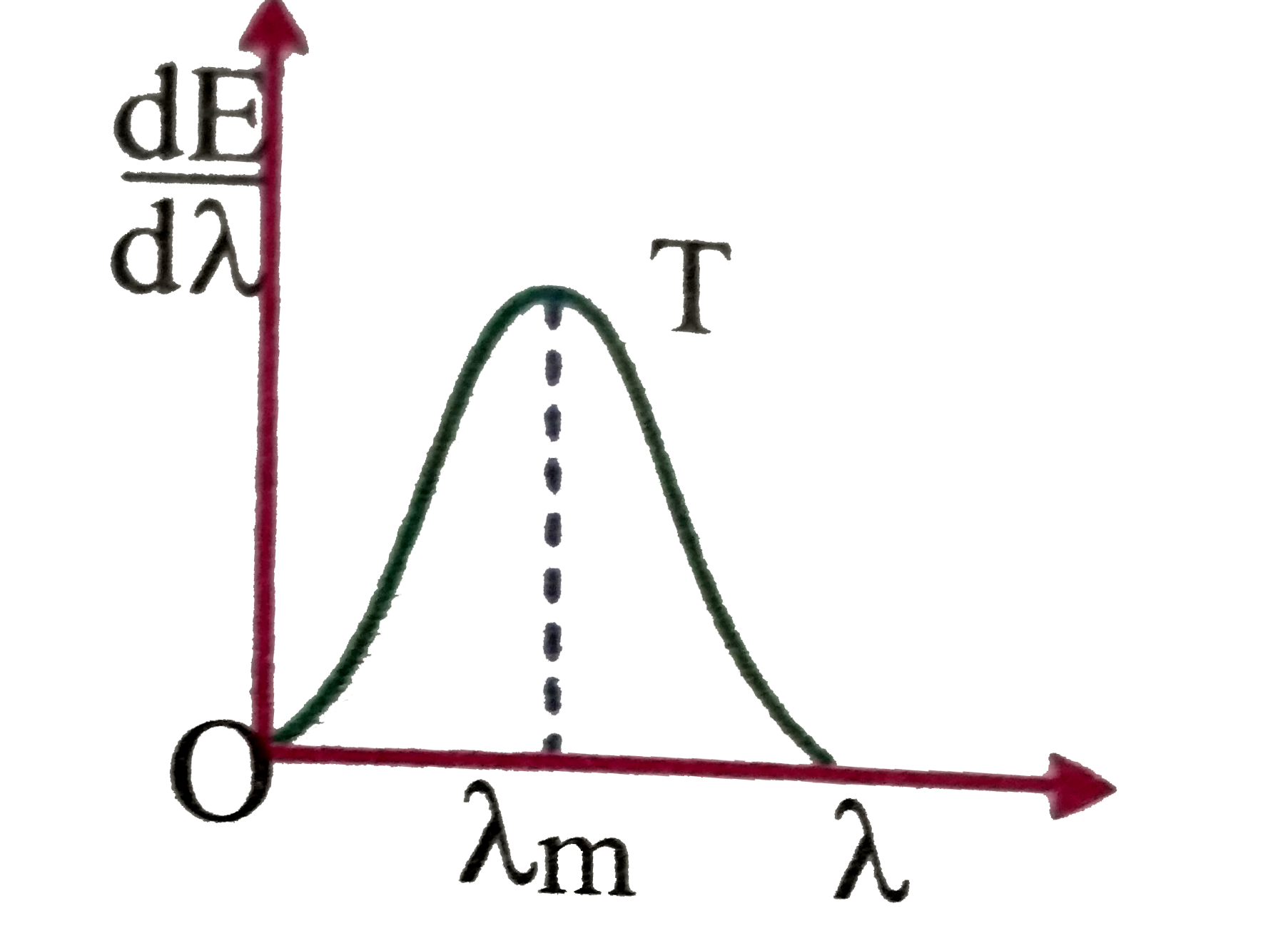
Choose the correct statements (s) .
View Solution
Knowledge Check
The minimum temperature of a body at which it emits light is
A1200∘ CB1000∘ CC500∘ CD200∘ CThe rate at which a black body emits radiation at a temperature T is proportional to
A1TBTCT3DT4The rate at which a black body emits radiation at a temperature T is proportional to
A1TBTCT3DT4
The energy emitted per second by a black body at 27∘C is 10 J. If the temperature of the black body is increased to 327∘C , the energy emitted per second will be
View SolutionA heated body emits radiation which has maximum intensity at frequency vm If the temperature of the body is doubled:
View SolutionA black body is at temperature of 500K. It emits energy at rate which is proportional to
View SolutionA black body is at a temperature 300K. It emits energy at a rate, which is proportional to
View SolutionStatement-1 : As temperature of a black body is raised, wavelenght corresponding to which energy emitted is maximum, reduces.
Statement-2 : Higher temperature would mean higher energy and hence higher wavelength.
View Solution
