The heat developed in a system is proportional to the current through it.
It cannot be Thomson heat.
It cannot be Peltier heat.
It cannot be Joule heat.
It can be any of the three heats mentioned above.
The correct Answer is:C
To solve the problem, we need to analyze the relationship between heat developed in a system and the current flowing through it based on Joule's law of heating.
1. Understanding the Problem Statement:
The problem states that the heat developed in a system is proportional to the current through it. We need to determine if this statement aligns with Joule's law.
2. Recall Joule's Law:
According to Joule's law, the heat (H) generated in a conductor is given by the formula:
H=I2Rt
where:
- H is the heat developed,
- I is the current,
- R is the resistance,
- t is the time for which the current flows.
3. Analyzing the Proportionality:
From Joule's law, we see that heat is proportional to the square of the current (I2). This means:
H∝I2
However, the question states that heat is directly proportional to the current (H∝I).
4. Conclusion:
Since Joule's law indicates that heat is proportional to the square of the current, the statement in the question cannot be true if we are considering Joule heating. Therefore, the heat developed in a system cannot be simply proportional to the current.
5. Final Answer:
The answer is that the heat developed in a system is not directly proportional to the current according to Joule's law.
The problem states that the heat developed in a system is proportional to the current through it. We need to determine if this statement aligns with Joule's law.
According to Joule's law, the heat (H) generated in a conductor is given by the formula:
H=I2Rt
where:
- H is the heat developed,
- I is the current,
- R is the resistance,
- t is the time for which the current flows.
From Joule's law, we see that heat is proportional to the square of the current (I2). This means:
H∝I2
However, the question states that heat is directly proportional to the current (H∝I).
Since Joule's law indicates that heat is proportional to the square of the current, the statement in the question cannot be true if we are considering Joule heating. Therefore, the heat developed in a system cannot be simply proportional to the current.
The answer is that the heat developed in a system is not directly proportional to the current according to Joule's law.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Objective 25videos
THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENT
- BOOK - HC VERMA ENGLISHCHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Exercise24videos
THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENT
- BOOK - HC VERMA ENGLISHCHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Worked out example8videos
THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENT
- BOOK - HC VERMA ENGLISHCHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Short answer2videos
THE SPECIAL THEORY OF RELATIVITY
- BOOK - HC VERMA ENGLISHCHAPTER - X-RaysEXERCISE - Ques for Short Ans10videos
X-Rays
Similar Questions
Statement I : If the current of a lamp increases by 20%, the percentage increases in the illlumination of the lamp is 40%.
Statement II : Illumination of the lamp is directly proportional to the square of the current through the lamp.View SolutionIn the series LCR circuit as shown in figure, the heat developed in 80 seconds and amplitude of wattless current is :
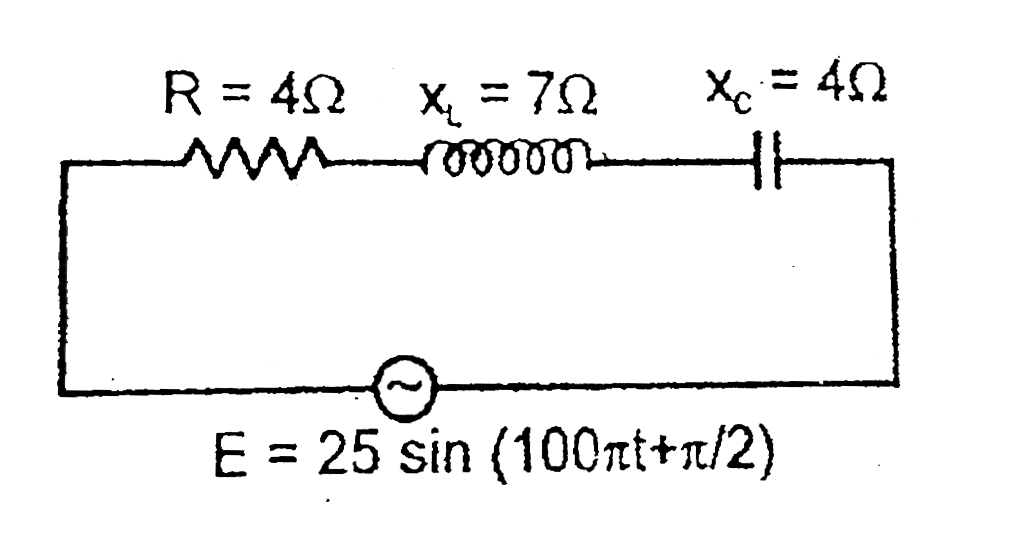 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Assertion: current sensitivity of a galvanometer is directly proportional to the current through the coil.
Reason: Voltage sensitivity is inversely proportional to voltage.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion is false but reason is true
Statement I: The specific heat of a gas in an adiabatic process is zwero but it is infinite in an isothermal process.
Statement II: Specific heat of a gas is directly proportional to heat exchanged with the system and inversely proportional to change in termperature.View SolutionStatement I: The specific heat of a gas in an adiabatic process is zwero but it is infinite in an isothermal process.
Statement II: Specific heat of a gas is directly proportional to heat exchanged with the system and inversely proportional to change in termperature.View SolutionWho developed the system of binomial nomenclature?
View Solutioncalculate the heat absorbed by a system in going through the cyclic process shown in ,
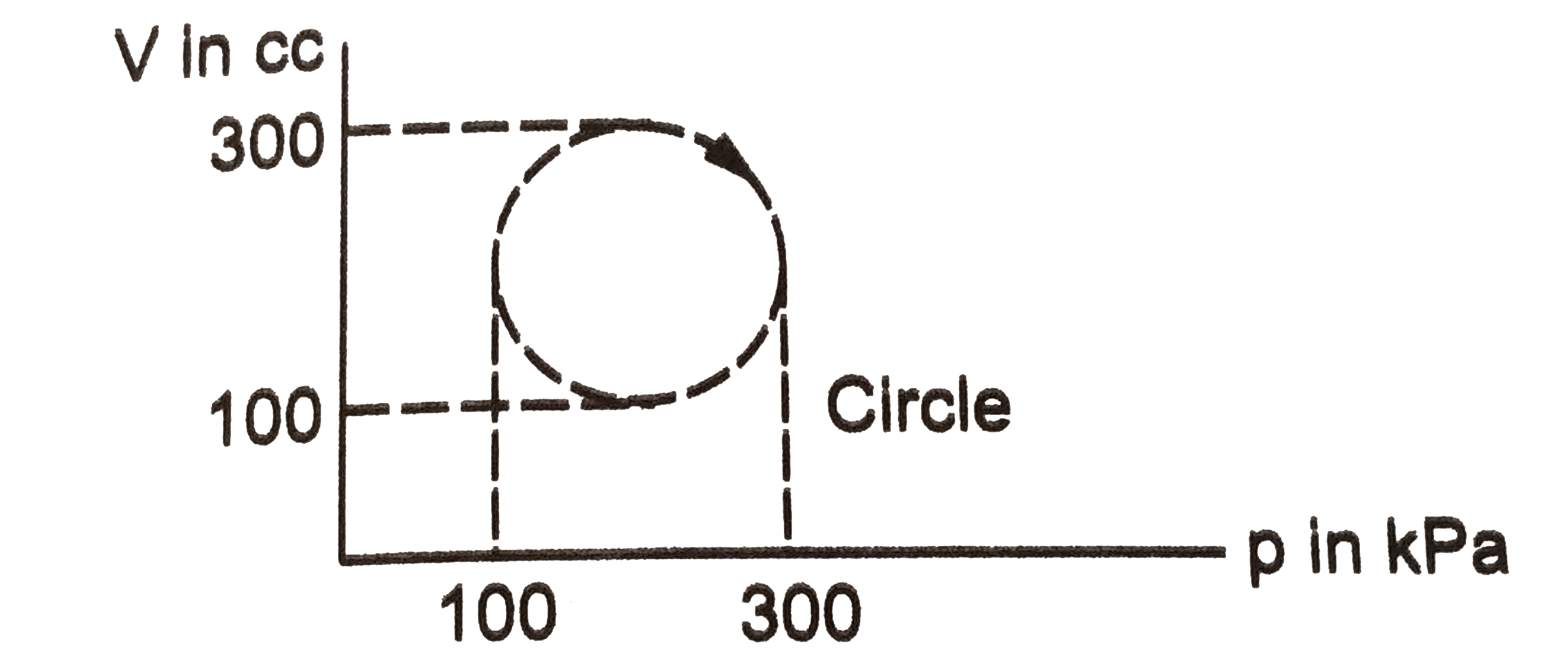 View Solution
View SolutionCalculate the heat abosrbed by a system in going through the cyclic process show in Fig.
 View Solution
View SolutionCalculate the heat abosrbed by a system in going through the cyclic process show in Fig.
 View Solution
View SolutionThe heat developed in a system is proportional to the current through it.
View Solution

