The height of mercury which exerts the same pressure as 20 cm of water column, is
1.47 cm
14.8 cm
148 cm
none of these
The correct Answer is:A
Pressure = hdg
∴ Let height of mercury be h cm.
Then h×13.6×g=20×1×g
⇒h=2013.6=1.47cm
Topper's Solved these Questions
- FORCE AND PRESSURE BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - FORCE AND PRESSURE EXERCISE - Self Assessment Sheet
11 Videos
- FORCE AND PRESSURE BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - FORCE AND PRESSURE EXERCISE - Self Assessment Sheet
11 Videos
- ELECTRICITYBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - ELECTRICITYEXERCISE - SELF ASSESSMENT SHEET
22 Videos
- LIGHTBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - LIGHTEXERCISE - SELF ASSESSMENT SHEET -4
24 Videos
Similar Questions
Knowledge Check
The height of mercury column of a barometer at the sea level is
A76 mB76 cmC1 mD0.76 mmWhich of the following water columns exerts the highest pressure on the bottom of the container?
A10 kmB100 mC1000 mmD5000 m
The height of the mercury column in a barometer at a place is 75 cm. If a liquid of unknown density is used the height of the liquid column is 150 cm, find its density.
View SolutionThe height of the mercury column in a barometer at a place is 75 cm. If a liquid of unknown density is used the height of the liquid column is 150 cm, find its density.
View SolutionA barometer tube is inclined at an angle of 30∘ with horizontal direction. Calculate length of mercury column in tube if atmospheric pressure is 76 cm of mercury.
View SolutionThe length of water column that can exert 1 atm pressure is ________ .
View SolutionSuppose water is used in a barometer instead of mercury. If the barometric pressure is 760mmHg, what is the height of the water column in the barometer at 0∘C. The densities of water and mercury at 0∘C are 0.99987gcm−3 and 13.596gcm−3 , respectively.
Strategy : The prtessure exerted by a column of liquid h whose density is d is hdg. Because the pressure are equal , we can equate the expressions for water (W) and mercury (M):
hWdWg=hMdMg
or hWdW=hMdM
Rearranging gives
hWhM=dMdW
This implies that the height of the liquid column in inversely proportional to its density . Solve the equation to find the height of the water column, hW.
View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
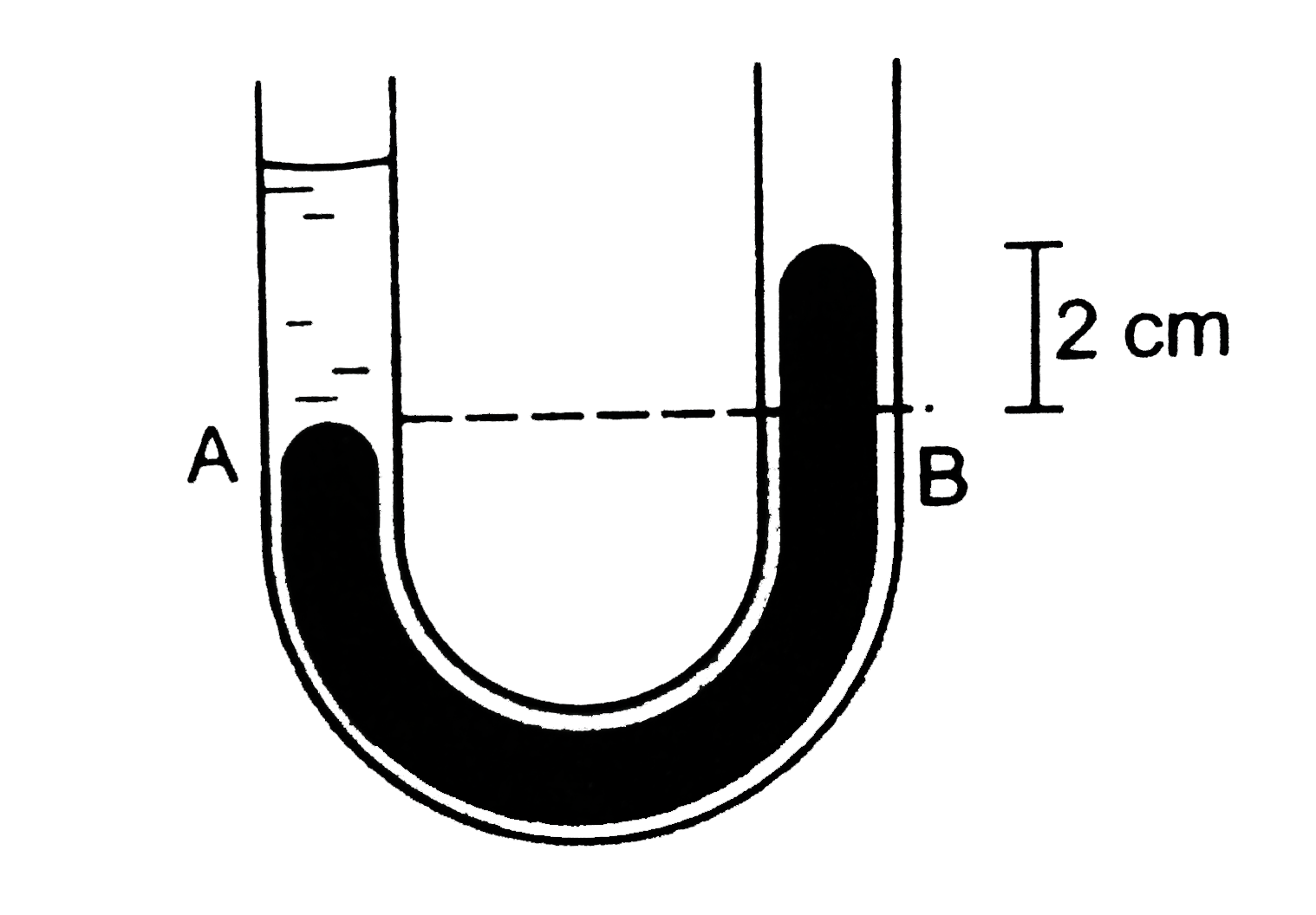 ,
,
View Solution
