The hydrogen atom in its ground state is excited by means of monochromatic radiation. Its resulting spectrum has six different lines. These radiations are incident on a metal plate. It is observed that only two of them are responsible for photoelectric effect. if the ratio of maximum kinetic energy of photoelectrons is the two cases is 5 then find the work function of the metal.
The correct Answer is:A, B
To solve the problem step by step, we will follow the reasoning outlined in the video transcript while providing a clear structure for the calculations.
Step 1: Understand the Problem
The problem states that a hydrogen atom in its ground state is excited, resulting in six spectral lines. Two of these lines are responsible for the photoelectric effect, and the ratio of the maximum kinetic energies of the photoelectrons from these two lines is given as 5.
Step 2: Set Up the Kinetic Energy Equation
Let the maximum kinetic energies of the photoelectrons from the two transitions be K1 and K2. According to the problem, we have:
K1K2=5
This implies:
K1=5K2
Step 3: Relate Kinetic Energy to Energy Transitions
The kinetic energy of photoelectrons can be expressed in terms of the energy of the incident photons and the work function W of the metal:
K1=E1−WandK2=E2−W
where E1 and E2 are the energies of the photons corresponding to the two transitions.
Step 4: Substitute the Kinetic Energy Expressions
Substituting the expressions for K1 and K2 into the ratio, we get:
E1−WE2−W=5
Step 5: Cross Multiply
Cross-multiplying gives:
E1−W=5(E2−W)
Expanding this, we have:
E1−W=5E2−5W
Rearranging terms leads to:
E1=5E2−4W
Step 6: Determine Energy Levels
From the hydrogen atom, the energy levels are given by:
En=−13.6eVn2
For n=4:
E4=−13.616=−0.85eV
For n=3:
E3=−13.69=−1.51eV
For n=2:
E2=−13.64=−3.4eV
For n=1:
E1=−13.6eV
Step 7: Calculate the Energy Differences
Now we calculate the energy differences for the transitions:
1. From n=4 to n=1:
ΔE1=E4−E1=−0.85−(−13.6)=12.75eV
2. From n=3 to n=1:
ΔE2=E3−E1=−1.51−(−13.6)=12.09eV
Step 8: Substitute Energy Differences into the Equation
Substituting these values into our earlier equation:
12.75−W12.09−W=5
Step 9: Cross Multiply Again
Cross-multiplying gives:
12.75−W=5(12.09−W)
Expanding this:
12.75−W=60.45−5W
Rearranging gives:
4W=60.45−12.75
4W=47.7
W=47.74=11.925eV
Conclusion
The work function W of the metal is approximately 11.925eV.
The problem states that a hydrogen atom in its ground state is excited, resulting in six spectral lines. Two of these lines are responsible for the photoelectric effect, and the ratio of the maximum kinetic energies of the photoelectrons from these two lines is given as 5.
Let the maximum kinetic energies of the photoelectrons from the two transitions be K1 and K2. According to the problem, we have:
K1K2=5
This implies:
K1=5K2
The kinetic energy of photoelectrons can be expressed in terms of the energy of the incident photons and the work function W of the metal:
K1=E1−WandK2=E2−W
where E1 and E2 are the energies of the photons corresponding to the two transitions.
Substituting the expressions for K1 and K2 into the ratio, we get:
E1−WE2−W=5
Cross-multiplying gives:
E1−W=5(E2−W)
Expanding this, we have:
E1−W=5E2−5W
Rearranging terms leads to:
E1=5E2−4W
From the hydrogen atom, the energy levels are given by:
En=−13.6eVn2
For n=4:
E4=−13.616=−0.85eV
For n=3:
E3=−13.69=−1.51eV
For n=2:
E2=−13.64=−3.4eV
For n=1:
E1=−13.6eV
Now we calculate the energy differences for the transitions:
1. From n=4 to n=1:
ΔE1=E4−E1=−0.85−(−13.6)=12.75eV
2. From n=3 to n=1:
ΔE2=E3−E1=−1.51−(−13.6)=12.09eV
Substituting these values into our earlier equation:
12.75−W12.09−W=5
Cross-multiplying gives:
12.75−W=5(12.09−W)
Expanding this:
12.75−W=60.45−5W
Rearranging gives:
4W=60.45−12.75
4W=47.7
W=47.74=11.925eV
The work function W of the metal is approximately 11.925eV.
Topper's Solved these Questions
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Passage 4
1 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MODERN PHYSICS - 2BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Subjective
10 Videos
Similar Questions
The hydrogen atom in the ground state is excited by means of monochromatic radiation of wavelength xA0 The resulting spectrum consists of 15 different lines. Calculate the value of x.
View SolutionHydrogen atom in its ground state is excited by means of monochromatic radiation of wavelength 975A∘. How many different lines are possible in the resulting spectrum? Calculate the longest wavelength amongst them.
View SolutionHydrogen atom in ground state is excited by a monochromatic radiation of λ=975Å. Number of spectral lines in the resulting spectrum emitted will be
View SolutionThe hydrogen atom in the ground state is excited by mass of monochromatic radiations of wavelength
λÅ . The resulting spectrum consists of maximum 15 different lines . What is the value of λ ? (RH=109737cm−1).
View SolutionHydrogen atom is ground state is excited by mean of monochromatic radiation of wavelength 975Å How many different lines are possible in the resulting spectrum ? Calculate the longest wavelength for hydrogen atom as ionization energy is13.6eV
View SolutionHydrogen atom is its ground state is excited by means of monochromatic radiation of wavelength 1023Å. How many different lines are possible in the resulting spectrum? Calculate the longes wavelength among them. You may assume the ionization energy of hydrogen atom as 13.6 eV.
View SolutionIn an experiment of photo-electric effect, the graph of maximum kinetic energy Ek of the emitted photoelectrons versus the frequency v of the incident light is a straight line AB as shown in figure below :
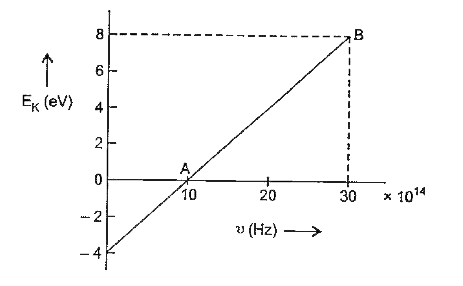
Work function of the metal.
View SolutionRadiations of two photon’s energy, twice and ten times the work function of metal are incident on the metal surface successsively. The ratio of maximum velocities of photoelectrons emitted in two cases is
View SolutionAn H- atom in the ground state is excited by monochromatic radiation of photon energy 13.056 eV. The number of emission lines will be (given its ionisation energy is 13.6 eV)
View SolutionThe surface of a metal is illuminated alternately with photons of energies E1=4eV and E2=2.5eV respectively. The ratio of maximum speeds of the photoelectrons emitted in the two cases is 2. The work function of the metal in (eV) is ________.
View Solution
