The ionisation energy of isolated pentavalent phosphorous atom is very large. How is it possible that when it goes into silicon lattice position to ralease its fifth electron at room temperature so that n-type semiconductor is obtained?
To understand how phosphorus can release its fifth electron in a silicon lattice to form an n-type semiconductor despite its high ionization energy, we can break down the explanation into several steps:
Step 1: Understanding Phosphorus and Silicon
- Phosphorus (P) is a pentavalent element, meaning it has five valence electrons. Silicon (Si) is tetravalent with four valence electrons.
- When phosphorus is introduced into the silicon lattice, it replaces a silicon atom.
Hint: Remember that the valency of an element indicates how many electrons it can share or bond with other atoms.
Step 2: Bonding in Silicon Lattice
- In the silicon lattice, phosphorus will form four covalent bonds with neighboring silicon atoms using four of its five valence electrons.
- This leaves one electron (the fifth electron) associated with phosphorus that is not involved in bonding.
Hint: Consider how the bonding structure of silicon affects the electrons of the dopant atom (phosphorus).
Step 3: Energy Consideration of the Fifth Electron
- The fifth electron that remains unbonded is loosely bound to the phosphorus atom. Although phosphorus has a high ionization energy in isolation, the energy required to free this loosely bound electron in the silicon lattice is much lower.
- At room temperature, thermal energy can provide sufficient energy to overcome this small binding energy.
Hint: Think about how temperature affects the energy states of electrons in a solid.
Step 4: Ionization Energy in the Context of Silicon
- The effective ionization energy for the fifth electron in the silicon lattice is significantly reduced. For example, the calculated ionization energy in silicon is approximately 0.1 eV.
- This is much lower than the ionization energy of isolated phosphorus, making it feasible for the fifth electron to be released at room temperature.
Hint: Compare the ionization energy in isolation versus in a lattice to see how the environment influences electron behavior.
Step 5: Formation of n-Type Semiconductor
- Once the fifth electron is freed, it becomes a conduction electron, contributing to electrical conductivity.
- In n-type semiconductors, these conduction electrons are the majority carriers, allowing the material to conduct electricity.
Hint: Recall the definition of n-type semiconductors and the role of majority carriers in conductivity.
Summary
In summary, while the ionization energy of isolated phosphorus is high, the environment of the silicon lattice allows for the fifth electron to be released with relatively low energy. This process leads to the formation of an n-type semiconductor, where electrons serve as the majority carriers.
- Phosphorus (P) is a pentavalent element, meaning it has five valence electrons. Silicon (Si) is tetravalent with four valence electrons.
- When phosphorus is introduced into the silicon lattice, it replaces a silicon atom.
- In the silicon lattice, phosphorus will form four covalent bonds with neighboring silicon atoms using four of its five valence electrons.
- This leaves one electron (the fifth electron) associated with phosphorus that is not involved in bonding.
- The fifth electron that remains unbonded is loosely bound to the phosphorus atom. Although phosphorus has a high ionization energy in isolation, the energy required to free this loosely bound electron in the silicon lattice is much lower.
- At room temperature, thermal energy can provide sufficient energy to overcome this small binding energy.
- The effective ionization energy for the fifth electron in the silicon lattice is significantly reduced. For example, the calculated ionization energy in silicon is approximately 0.1 eV.
- This is much lower than the ionization energy of isolated phosphorus, making it feasible for the fifth electron to be released at room temperature.
- Once the fifth electron is freed, it becomes a conduction electron, contributing to electrical conductivity.
- In n-type semiconductors, these conduction electrons are the majority carriers, allowing the material to conduct electricity.
In summary, while the ionization energy of isolated phosphorus is high, the environment of the silicon lattice allows for the fifth electron to be released with relatively low energy. This process leads to the formation of an n-type semiconductor, where electrons serve as the majority carriers.
Topper's Solved these Questions
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - SAMPLE PROBLEM
2 Videos
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - CONCEPTUAL PROBLEMS
1 Videos
- ELECTROMAGNETIC WAVESBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question
5 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS
2 Videos
Similar Questions
Read the pasage given below as well as the adjoining energy level diagram and then answer the questions given after the passage .
As per Bohr's theory og hydrogen atom the energy of an atom in a state corresponding to principal quantum number n is given as :
En=−13.6n2eV
The energy of an atom is the least when its electron is revolving in an orbit closets to the nucleus i.e., the one for which n =1. This state is called the ground state. When a hydrogen atom receives energy by processes such as electron collision , the atom may acquire sufficient energy to raise the electron to higher energy states and the atom is then said to be in an excited state . From these excited states the electron can then fall back to a state of lower energy , emitting a photon in the process.
The energy level diagram for the stationary states of a hydrogen atom , compouted from Bohr's relation for energy , is given in Fig.12.02. The principal quantum number n labels the stationary states in the ascending order of energy . Obviously , the highest energy corresponds to n=∞ and has an energy of 0 eV. This is the energy of the atom when the electron is completely removed (r=∞) from the nucleus and is at rest.
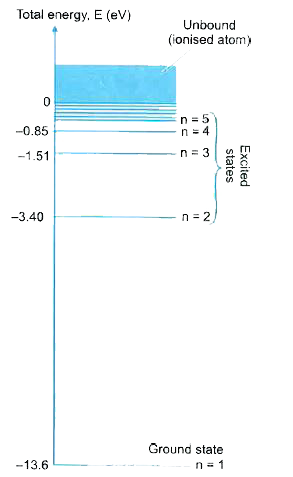
Now answer the follwoing questions:
Define ionisation energy of hydrogen atom and give its value.
View SolutionRead the pasage given below as well as the adjoining energy level diagram and then answer the questions given after the passage .
As per Bohr's theory og hydrogen atom the energy of an atom in a state corresponding to principal quantum number n is given as :
En=−13.6n2eV
The energy of an atom is the least when its electron is revolving in an orbit closets to the nucleus i.e., the one for which n =1. This state is called the ground state. When a hydrogen atom receives energy by processes such as electron collision , the atom may acquire sufficient energy to raise the electron to higher energy states and the atom is then said to be in an excited state . From these excited states the electron can then fall back to a state of lower energy , emitting a photon in the process.
The energy level diagram for the stationary states of a hydrogen atom , compouted from Bohr's relation for energy , is given in Fig.12.02. The principal quantum number n labels the stationary states in the ascending order of energy . Obviously , the highest energy corresponds to n=∞ and has an energy of 0 eV. This is the energy of the atom when the electron is completely removed (r=∞) from the nucleus and is at rest.

Now answer the follwoing questions:
How can a hydrogen atom receive energy to raise the electron to higher energy states ?
View Solution
Knowledge Check
DEFINITION VALID FOR SINGLE ELECTRON SYSTEM :
Ground state:
Lowest energy state of any atom or ion is called ground state of the atom.It is n=1.
Excited State :
States of atom other than the ground state are called excited states.
Ionisation energy (IE):
Minimum energy required to move an electron from ground state to n=∞ is called ionisation energy of the atom or ion.
Ionisation Potential (I.P) :
Potential difference through which a free electron must be accelerated from rest, such that its kinetic energy becomes equal to ionisation energy of the atom is called ionisation potential of the atom.
Excitation Energy :
Energy required to move an electron from ground state of the atom to the atom is called excitation energy of that state.
Excitation Potential :
Potentail difference through which an electron must be accelerated from rest to so that its kinetic energy becomes equal to excitation energy of any state is called excitation potentail of that state.
Binding Energy 'or' Seperation Energy :
Energy required to move an electron from any state to n=∞ is called binding energy of that state.
If the wavelength of photon emitted from an electron jump n=4 to n=2 in a H-like species is 1216Å, then the species is :AH-atomBHe+ ionCLi2+ ionDBe3+ ionDEFINITION VALID FOR SINGLE ELECTRON SYSTEM :
Ground state:
Lowest energy state of any atom or ion is called ground state of the atom.It is n=1.
Excited State :
States of atom other than the ground state are called excited states.
Ionisation energy (IE):
Minimum energy required to move an electron from ground state to n=∞ is called ionisation energy of the atom or ion.
Ionisation Potential (I.P) :
Potential difference through which a free electron must be accelerated from rest, such that its kinetic energy becomes equal to ionisation energy of the atom is called ionisation potential of the atom.
Excitation Energy :
Energy required to move an electron from ground state of the atom to the atom is called excitation energy of that state.
Excitation Potential :
Potentail difference through which an electron must be accelerated from rest to so that its kinetic energy becomes equal to excitation energy of any state is called excitation potentail of that state.
Binding Energy 'or' Seperation Energy :
Energy required to move an electron from any state to n=∞ is called binding energy of that state.
If the I excitation potential of a hypothetical H-like is 62 V, then the value of II excitation energy is about :A192 eVB30 eVC216 eVD40.5 eVDEFINITION VALID FOR SINGLE ELECTRON SYSTEM :
Ground state:
Lowest energy state of any atom or ion is called ground state of the atom.It is n=1.
Excited State :
States of atom other than the ground state are called excited states.
Ionisation energy (IE):
Minimum energy required to move an electron from ground state to n=∞ is called ionisation energy of the atom or ion.
Ionisation Potential (I.P) :
Potential difference through which a free electron must be accelerated from rest, such that its kinetic energy becomes equal to ionisation energy of the atom is called ionisation potential of the atom.
Excitation Energy :
Energy required to move an electron from ground state of the atom to the atom is called excitation energy of that state.
Excitation Potential :
Potentail difference through which an electron must be accelerated from rest to so that its kinetic energy becomes equal to excitation energy of any state is called excitation potentail of that state.
Binding Energy 'or' Seperation Energy :
Energy required to move an electron from any state to n=∞ is called binding energy of that state.
If the binding energy of II excitec state of a H-like species is 13.6 eV, then:AThe atomic number Z of given a H-like species is 2BA photon of energy 30 eV can ionise an electron from I excited state of given H-like speciesCUpon de-excitation from n=4 to n=2 is given H-like species, the emitted photon has wavenumber v=3R16(R=Rydber's constant)DIonisation potential of given H-like species is 122.4 V
A cylindrical copper conductor AB length L areaa of cross-section a has large number of free electrons which at mean temperature move at random within the body of the conductor like the molecules of a gas. The average thermal motion at room temperature is of the enter of 105ms−1 where a potential difference V is applied free electronic in the condictior experience , the free electrons in the conductor experience force and are accelerated towards the positive emf of the condutor on their gained kinetic energy After each collision the free electronic are angle acceleration due of the electric field , towards the positive end the conductor and next collision with the ions/atoms of the electrons The average speed of the free electrons with which they drift toward the positive and of the conductor under the effect of applied electric field is called drift of the electrons
The speed of electrons in a conductor is small (=10−4ms−1) when the switch is closed, the bulb at a distance glows immediately. It is so because
View SolutionRead the following text and answer the following questions on the basis of the same:
Band theory of solid:
Consider that the Si or Ge crystal contains N atoms. Electrons of each atom will have discrete energies in different orbits. The electron energy will be same if all the atoms are isolated, i.e., separated from each other by a large distance. However, in a crystal, the atoms are close to each other (2 Å to 3 Å) and therefore the electrons interact with each other and also with the neighbouring atomic cores. The overlap (or interaction) will be more felt by the electrons in the outermost orbit while the inner orbit or core electron energies may remain unaffected. Therefore, for understanding electron energies in Si or Ge crystal, we need to consider the changes in the energies of the electrons in the outermost orbit only. For Si, the outermost orbit is the third orbit (n = 3), while for Ge it is the fourth orbit (n = 4). The number of electrons in the outermost orbit is 4 (2s and 2p electrons). Hence, the total number of outer electrons in the crystal is 4N. The maximum possible number of outer electrons in the orbit is 8 (2s + 6p electrons). So, out of the 4N electrons, 2N electrons are in the 2N s-states (orbital quantum number l = 0) and 2N electrons are in the available 6N p-states. Obviously, some p-electron states are empty. This is the case of well separated or isolated atoms.
For Silicon and Germanium the outermost orbits are respectively:
View SolutionRead the following text and answer the following questions on the basis of the same:
Band theory of solid:
Consider that the Si or Ge crystal contains N atoms. Electrons of each atom will have discrete energies in different orbits. The electron energy will be same if all the atoms are isolated, i.e., separated from each other by a large distance. However, in a crystal, the atoms are close to each other (2 Å to 3 Å) and therefore the electrons interact with each other and also with the neighbouring atomic cores. The overlap (or interaction) will be more felt by the electrons in the outermost orbit while the inner orbit or core electron energies may remain unaffected. Therefore, for understanding electron energies in Si or Ge crystal, we need to consider the changes in the energies of the electrons in the outermost orbit only. For Si, the outermost orbit is the third orbit (n = 3), while for Ge it is the fourth orbit (n = 4). The number of electrons in the outermost orbit is 4 (2s and 2p electrons). Hence, the total number of outer electrons in the crystal is 4N. The maximum possible number of outer electrons in the orbit is 8 (2s + 6p electrons). So, out of the 4N electrons, 2N electrons are in the 2N s-states (orbital quantum number l = 0) and 2N electrons are in the available 6N p-states. Obviously, some p-electron states are empty. This is the case of well separated or isolated atoms.
The maximum possible electrons in an orbit is:
View SolutionRead the following text and answer the following questions on the basis of the same:
Band theory of solid:
Consider that the Si or Ge crystal contains N atoms. Electrons of each atom will have discrete energies in different orbits. The electron energy will be same if all the atoms are isolated, i.e., separated from each other by a large distance. However, in a crystal, the atoms are close to each other (2 Å to 3 Å) and therefore the electrons interact with each other and also with the neighbouring atomic cores. The overlap (or interaction) will be more felt by the electrons in the outermost orbit while the inner orbit or core electron energies may remain unaffected. Therefore, for understanding electron energies in Si or Ge crystal, we need to consider the changes in the energies of the electrons in the outermost orbit only. For Si, the outermost orbit is the third orbit (n = 3), while for Ge it is the fourth orbit (n = 4). The number of electrons in the outermost orbit is 4 (2s and 2p electrons). Hence, the total number of outer electrons in the crystal is 4N. The maximum possible number of outer electrons in the orbit is 8 (2s + 6p electrons). So, out of the 4N electrons, 2N electrons are in the 2N s-states (orbital quantum number l = 0) and 2N electrons are in the available 6N p-states. Obviously, some p-electron states are empty. This is the case of well separated or isolated atoms.
The energy of electrons of atoms of a substance will be same if:
View SolutionRead the following text and answer the following questions on the basis of the same:
Band theory of solid:
Consider that the Si or Ge crystal contains N atoms. Electrons of each atom will have discrete energies in different orbits. The electron energy will be same if all the atoms are isolated, i.e., separated from each other by a large distance. However, in a crystal, the atoms are close to each other (2 Å to 3 Å) and therefore the electrons interact with each other and also with the neighbouring atomic cores. The overlap (or interaction) will be more felt by the electrons in the outermost orbit while the inner orbit or core electron energies may remain unaffected. Therefore, for understanding electron energies in Si or Ge crystal, we need to consider the changes in the energies of the electrons in the outermost orbit only. For Si, the outermost orbit is the third orbit (n = 3), while for Ge it is the fourth orbit (n = 4). The number of electrons in the outermost orbit is 4 (2s and 2p electrons). Hence, the total number of outer electrons in the crystal is 4N. The maximum possible number of outer electrons in the orbit is 8 (2s + 6p electrons). So, out of the 4N electrons, 2N electrons are in the 2N s-states (orbital quantum number l = 0) and 2N electrons are in the available 6N p-states. Obviously, some p-electron states are empty. This is the case of well separated or isolated atoms.
The overlap (or interaction) will be more felt by the electrons when they are:
View Solution
