The kinetic energy of a particle executing SHM is 16J. When it is in its mean position. If the amplitude of oscillation is 25cm and the mass of the particle is 5.12 kg, the itme period of its oscillation in second is
π/5
2π
5π
20π
The correct Answer is:A
To solve the problem step by step, we will follow these steps:
Step 1: Understand the given information
- Kinetic Energy (KE) = 16 J
- Amplitude (A) = 25 cm = 0.25 m (convert to meters)
- Mass (m) = 5.12 kg
- Displacement (y) at mean position = 0 m
Step 2: Write the formula for kinetic energy in SHM
The kinetic energy of a particle in simple harmonic motion (SHM) is given by the formula:
KE=12mω2(A2−y2)
Since the particle is at the mean position, y=0. Therefore, the formula simplifies to:
KE=12mω2A2
Step 3: Substitute the known values into the kinetic energy equation
Substituting the known values into the equation:
16=12×5.12×ω2×(0.25)2
Calculating (0.25)2:
(0.25)2=0.0625
Now substituting this back into the equation:
16=12×5.12×ω2×0.0625
Step 4: Simplify the equation
First, calculate 12×5.12×0.0625:
12×5.12=2.56
2.56×0.0625=0.16
Now, we have:
16=0.16ω2
Step 5: Solve for ω2
Rearranging the equation to solve for ω2:
ω2=160.16=100
Step 6: Calculate ω
Taking the square root of both sides:
ω=√100=10 rad/s
Step 7: Calculate the time period T
The time period T is related to ω by the formula:
T=2πω
Substituting the value of ω:
T=2π10=π5 seconds
Final Answer
The time period of the oscillation is:
T=π5 seconds
---
- Kinetic Energy (KE) = 16 J
- Amplitude (A) = 25 cm = 0.25 m (convert to meters)
- Mass (m) = 5.12 kg
- Displacement (y) at mean position = 0 m
The kinetic energy of a particle in simple harmonic motion (SHM) is given by the formula:
KE=12mω2(A2−y2)
Since the particle is at the mean position, y=0. Therefore, the formula simplifies to:
KE=12mω2A2
Substituting the known values into the equation:
16=12×5.12×ω2×(0.25)2
Calculating (0.25)2:
(0.25)2=0.0625
Now substituting this back into the equation:
16=12×5.12×ω2×0.0625
First, calculate 12×5.12×0.0625:
12×5.12=2.56
2.56×0.0625=0.16
Now, we have:
16=0.16ω2
Rearranging the equation to solve for ω2:
ω2=160.16=100
Taking the square root of both sides:
ω=√100=10 rad/s
The time period T is related to ω by the formula:
T=2πω
Substituting the value of ω:
T=2π10=π5 seconds
The time period of the oscillation is:
T=π5 seconds
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Fill In The Blanks
20 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - PROBLEMS FOR PRACTICE
149 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Value Based Questions
5 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
The total energy of a particle of mass 0.1 kg performing SHM is 0.2 J . Find its maximum speed and period if the amplitude is 2cm.
View SolutionThe force on a body executing SHM is 4 N when the displacement from mean position is 2 cm. If amplitude of oscillation is 10 cm, then the maximum kinetic energy associated with the SHM will be
View Solution
Knowledge Check
The kinetic energy of a particle executing S.H.M. is 16 J when it is at its mean position. If the mass of the particle is 0.32 kg , then what is the maximum velocity of the particle
A5 m/sB15 m/sC10 m/sD20 m/sThe total energy of a particle executing SHM is E. Its kinetic energy is K at the mean position. Then always
AE−K=0BE−K<0CE−K>0DE−K≥0The total energy of a particle in SHM is E. Its kinetic energy at half the amplitude from mean position will be
AE/2BE/3CE/4D3E/4
The potential energy of a particle executing SHM in its rest position is 15 J. The average kinetic energy of the particle during one oscillation is 5 J. The total energy of the particle is
View SolutionThe potential energy of a particle execuring S.H.M. is 2.5 J, when its displacement is half of amplitude. The total energy of the particle be
View SolutionAcceleration -displacemnet graph of a particle executing SHM is as shown in given figure. The time period of its oscillations is (in s)
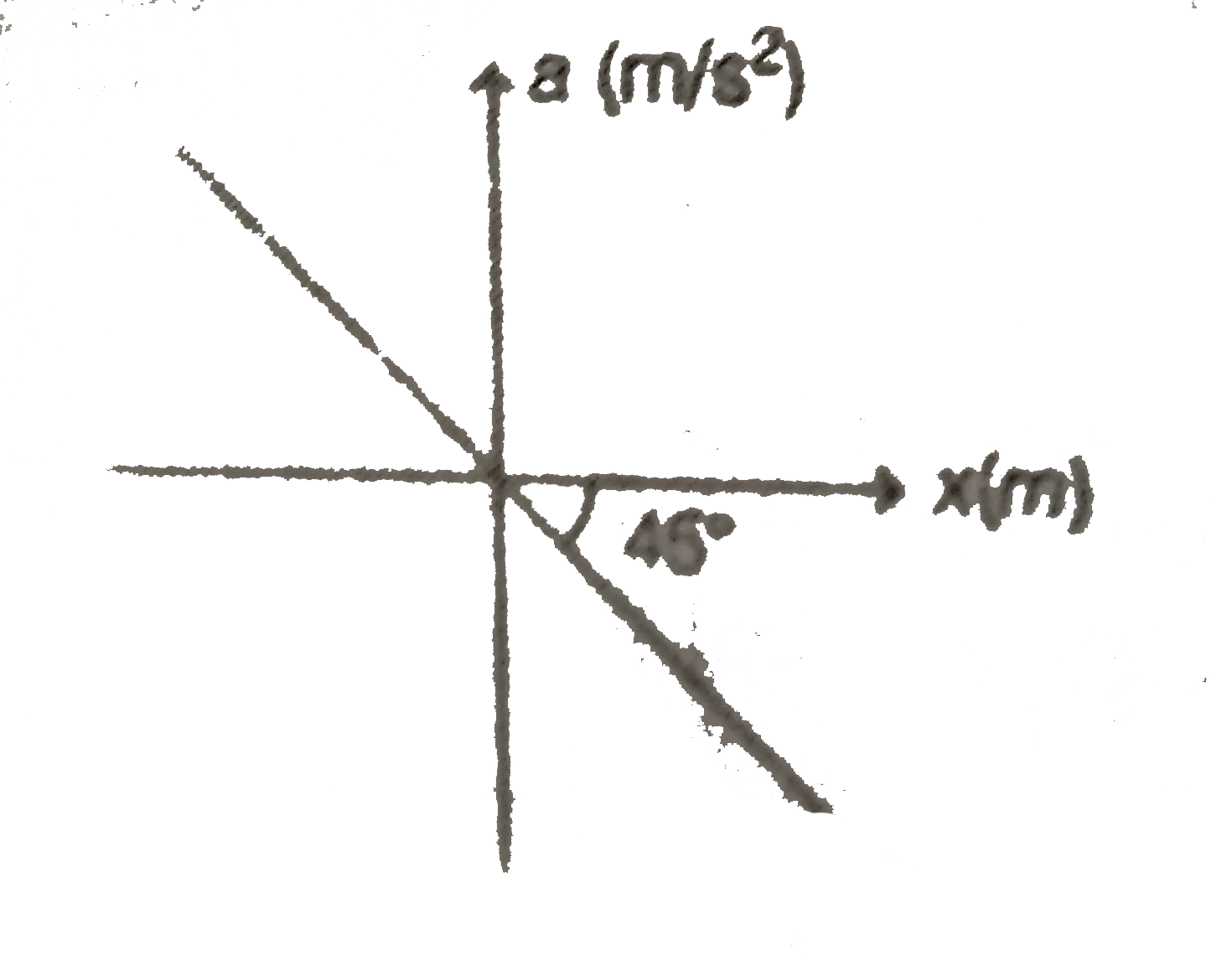
View SolutionA particle is executing SHM with an amplitude of 2 m. The difference in the magnitudes of its maximum acceleration and maximum velocity is 4. The time period of its oscillation is
View SolutionThe amplitude of a particle executing SHM is made three-fourth keeping its time period constant. Its total energy will be
View Solution
