The length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. Then natural length of the wire is
l1+l22
√(l1l2)
l1T2−l2T1T2−T1
l1T2−l2T1T1+T2
The correct Answer is:C
To find the natural length of the metal wire when given two different tensions and their corresponding lengths, we can use the relationship defined by Young's modulus. Here’s a step-by-step solution:
Step 1: Understand the relationship
We know that Young's modulus (Y) is defined as the ratio of stress to strain. Stress is given by TA (where T is the tension and A is the cross-sectional area), and strain is given by l−LL (where l is the extended length and L is the natural length).
Step 2: Set up equations for both tensions
For the first tension T1 and length l1:
Y=T1/A(l1−L)/L
This can be rearranged to:
Y=T1⋅LA⋅(l1−L)(Equation 1)
For the second tension T2 and length l2:
Y=T2/A(l2−L)/L
This can be rearranged to:
Y=T2⋅LA⋅(l2−L)(Equation 2)
Step 3: Equate the two expressions for Young's modulus
Since both expressions equal Y, we can set them equal to each other:
T1⋅LA⋅(l1−L)=T2⋅LA⋅(l2−L)
We can cancel A and L (assuming L is not zero) from both sides:
T1l1−L=T2l2−L
Step 4: Cross-multiply to solve for L
Cross-multiplying gives:
T1⋅(l2−L)=T2⋅(l1−L)
Expanding both sides:
T1⋅l2−T1⋅L=T2⋅l1−T2⋅L
Step 5: Rearranging to isolate L
Rearranging the equation to isolate L:
T1⋅l2−T2⋅l1=T1⋅L−T2⋅L
Factoring out L from the right side:
T1⋅l2−T2⋅l1=L⋅(T1−T2)
Step 6: Solve for L
Finally, we can solve for L:
L=T1⋅l2−T2⋅l1T1−T2
Conclusion
The natural length of the wire is given by:
L=T1⋅l2−T2⋅l1T1−T2
We know that Young's modulus (Y) is defined as the ratio of stress to strain. Stress is given by TA (where T is the tension and A is the cross-sectional area), and strain is given by l−LL (where l is the extended length and L is the natural length).
For the first tension T1 and length l1:
Y=T1/A(l1−L)/L
This can be rearranged to:
Y=T1⋅LA⋅(l1−L)(Equation 1)
Y=T2/A(l2−L)/L
This can be rearranged to:
Y=T2⋅LA⋅(l2−L)(Equation 2)
Since both expressions equal Y, we can set them equal to each other:
T1⋅LA⋅(l1−L)=T2⋅LA⋅(l2−L)
We can cancel A and L (assuming L is not zero) from both sides:
T1l1−L=T2l2−L
Cross-multiplying gives:
T1⋅(l2−L)=T2⋅(l1−L)
Expanding both sides:
T1⋅l2−T1⋅L=T2⋅l1−T2⋅L
Rearranging the equation to isolate L:
T1⋅l2−T2⋅l1=T1⋅L−T2⋅L
Factoring out L from the right side:
T1⋅l2−T2⋅l1=L⋅(T1−T2)
Finally, we can solve for L:
L=T1⋅l2−T2⋅l1T1−T2
The natural length of the wire is given by:
L=T1⋅l2−T2⋅l1T1−T2
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Integer Type Questions
12 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Asseration - Reason Type Question
18 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions-II
14 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
Knowledge Check
The length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. Then natural length of the wire is
Al1+l22B√l1l2Cl1T2−l2T1T2−T1Dl1T2+T1l2T2+T1The length of a steel wire is l1 when the stretching force is T1 and l2 when the stretching force is T2. The natural length of the wire is
Al1T1+l2T2T1+T2Bl2T1+l1T2T1+T2Cl2T1−l1T2T1−T2Dl1T1−l2T2T1−T2The length of a metal wire is 10cm when the tension in it is 20N and 12cm when the tension is 40N. Then natural length of the wire is in cm
A6B4C8D9
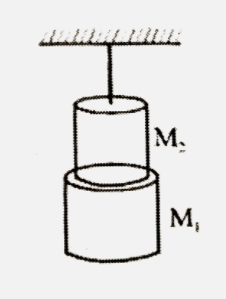
The length of wire, when M1 is hung from it, is l1 and is l2 with both M1 and M2 hanging. The natural length of wire is :-
View SolutionThe length of a metal wire is l when the tension is F and x l when the tension si y F. Then the natural length of the wire is
View SolutionWhen the tension in a metal wire is T1, its length is l1. When the tension is T2, its length is l2. The natural length of wire is
View SolutionThe length of a rubber cord is l1 m when the tension is 4 N and l2 m when the tension is 6 N.The length when the tension is 9 N, is
View SolutionThe length of a wire l1 when tension is 4 N and l2 when the tension is 5 N. Then its original length would be
View Solution
