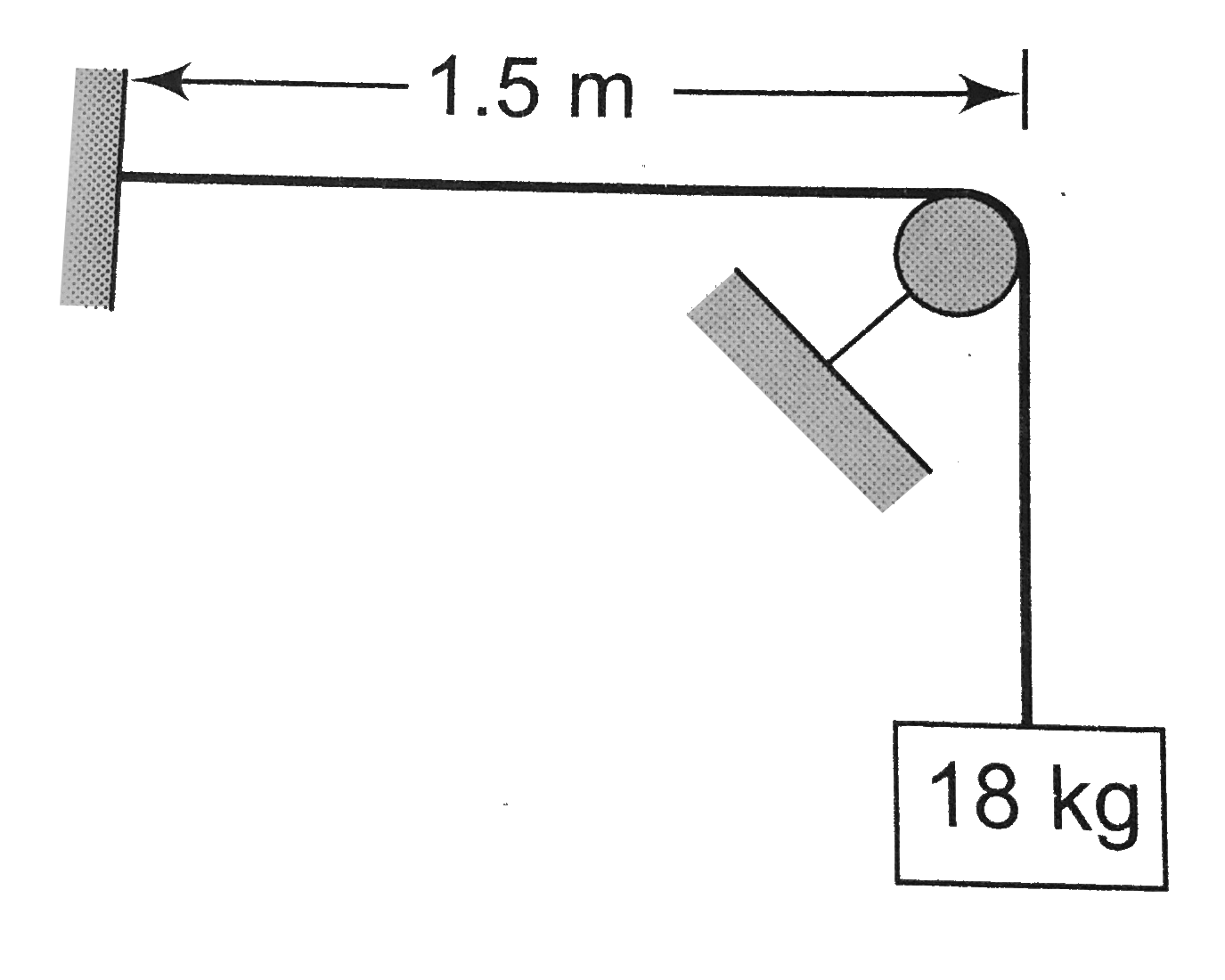
The length of the wire shown in Fig. Between the pulley and fixed support is 1.5m and mass is 12.0g the frequency of vibration with which the wire vibrate two loops leaving the middle point of the wire between the pulleys at rest is
10Hz
30Hz
100Hz
70Hz
The correct Answer is:C
f=22l√Tμ or f=1l√Tμ
or f=√TlMl2 or f=√TMl
or v=√18×10×100012×1.5Hz=100Hz.
Topper's Solved these Questions
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Vibration Of Air Column
23 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Sound Wave And Loudness
27 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Stationary Waves
20 Videos
- VECTORSBOOK - A2ZCHAPTER - VECTORSEXERCISE - Chapter Test
29 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Chapter Test
29 Videos
Similar Questions
The length of the wire shown in figure between the pulley is 1.5 m and its mass is 12.0 g. Find the frequency of vibration with which the wire vibrates in two loops leaving the middle point of the wire between the pulleys at rest.

View Solution(i) A wire is stretched between two rigid supports. It is observed that the wire resonates at a frequency of 420 Hz. If a wooden bridge is placed at the midpoint of the wire (so that the midpoint becomes a node), it was observed that the smallest frequency at which the wire resonates is 420 Hz. Find the smallest frequency at which the wire will resonate when there is no wooden bridge.
(ii) A string of length L is fixed at one end and is under tension due to a weight hanging from the other end, as shown in the figure. The point of the string on the pulley behaves as a fixed point. Coordinate axes are chosen so that the horizontal segment of the string runs from x=–L/2 to x=L/2. The string is vibrating at one of its resonant frequencies with transverse displacement (y) given by
y(x,t)=0.05cos(12.0x)sin(360t)
with x, y in meter and t in second. Write two smallest possible values of L consistent with the given equation?

View Solution
Knowledge Check
The length of the wire shown in figure between the pulleys is 1.5 m and its mass is 15 g. what is the frequency of vibration with which the wire vibrates in four loops leaving the middle point of the wire between the pullys at rest ? (g=10ms2)
 A1003HzB2003HzC4003HzD5003Hz
A1003HzB2003HzC4003HzD5003HzThe length of the wire shown in the figure between the pulleys is 1.5m and its mass is 12.0g. The frequency of vibration with which the wire vibrates in three loops forming antinode at the mid point of the wire is - (Take g=9.8m/s2)
 A210 HzB140 HzC70HzDnone of these
A210 HzB140 HzC70HzDnone of theseThe length of a sonometer wire tuned to a frequency of 250 Hz is 0.60 metre . The frequency of tuning fork with which the vibrating wire will be in tune when the length is made 0.40 metre is
A250 HzB375 HzC256 HzD384 Hz
The total length of a sonometer wire between fixed ends is 110 cm. To bridges are placed to divide the length of the wire in ratio 6 : 3 : 2. What is the minimum common frequency with which three parts can vibrate? Also calculate the ratio of number of loops formed in three parts. The tension in the wire is 400 N and the mass per unit length is 0.01kg/m .
View SolutionThe length of a sonometer wire between two fixed ends is 110cm. Where should the two bridges the placed so as to divide the wire into three segments, whose fundamental frequencies are in the ration1:2:3?
View SolutionA wire is under a tension of 32N and length between the two bridges in 1m. If the length of the sample wire is 10m and its mass is 2 g, then the fundamental frequency of the wire will be
View SolutionA sonometer wire is in tnison with a tuning fork of frequency 256 Hz, when the lenghts of the wire between the bridges is 75 cm and only one loop is formed. By keeping the lengths and tension constant, the wire is made to vibrate with 2 loops. The wire can still be in resonance with a tuning fork, provided the freqency of the tuning fork is
View SolutionA uniform wire of linear density 0.004 per kg-m, when stretched between two rigid supports, with a tension 3.6×102 N, resonates with a frequency of 420 hz. The next harmonic frequency with which the wire resonates is 490 Hz. The length of the wire in metre is
View Solution
