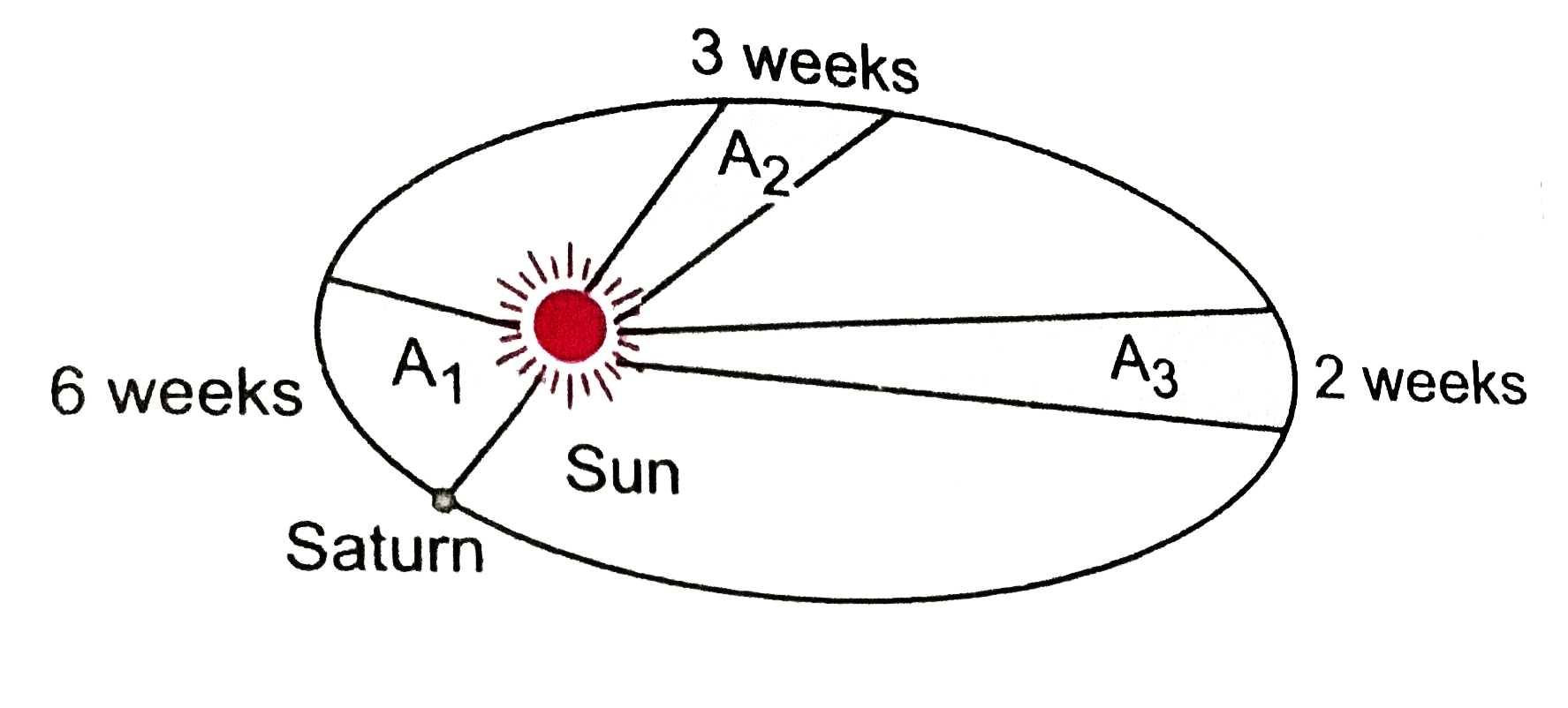
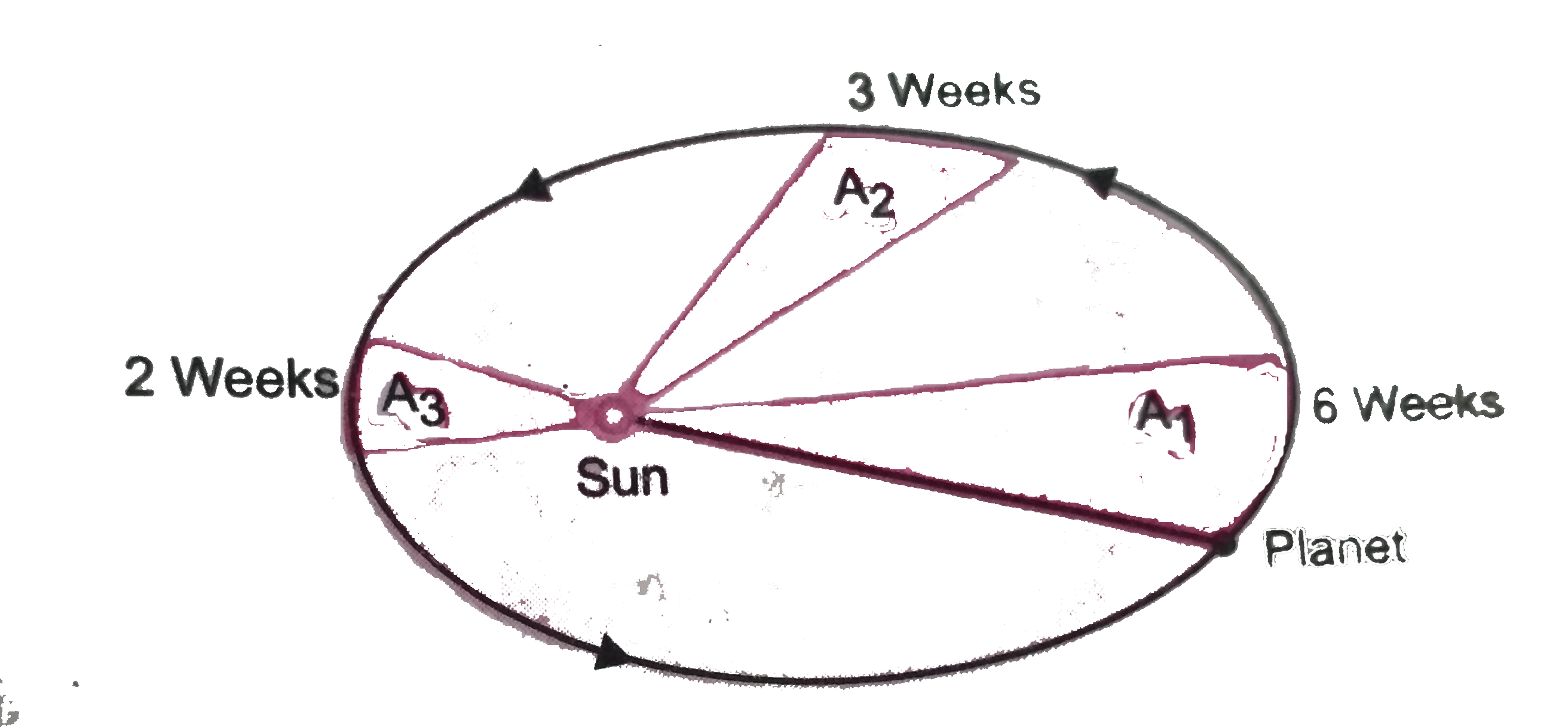
The line that joins the saturn to the sun sweeps area A1,A2 and A3 in time intervals of 6 weeks, 3 weeks and 2 weeks respectively as shows in the Fig. What is the correct relation between A1,A2 and A3?
Video Solution
Text Solution
According to kepler's law of area, the areal velocity of planet around the sun is constant. If A is the area swept by saturn in one weak, then
A1=6A,A2=3A and A3=2A
So, A1=2A2,A1=3A3
|
Topper's Solved these Questions
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - CONCEPTUAL PROBLEMS
36 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - CONCEPTUAL PROBLEMS II.
1 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - SOLVED EXAMPLES TYPE K
1 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Assertion - Reason Type questions
14 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
Similar Questions
Knowledge Check
A planet moving around the sun sweeps area A1 in 2 days, A2 in 4 days and A3 in 9 days. Then, relation between them
 AA1=A2=A3B9A1=3A2=2A3C18A1=9A2=4A3D3A1=4A2=6A3
AA1=A2=A3B9A1=3A2=2A3C18A1=9A2=4A3D3A1=4A2=6A3If A1,A2,A3 denote respectively the areas of an inscribed polygon of 2n sides , inscribed polygon of n sides and circumscribed poylgon of n sides ,then A1,A2,A3 are in
AA.P.BG.P.CH.P.Dnone of theseThree rectangles A1,A2 and A3 have the same area Their lengths a1,a2 and a3 respectively are such that a1<a2<a3. Cylinders C1,C2 and C3 are formed from A1,A2 and A3 respectively by joining the parallel sides along the breadth. Then,
 AC1 will enclose maximum volumeBC2 will enclose maximum volumeCC3 will enclose maximum volumeDEach of C1,C2 and C3 will enclose equal volume.
AC1 will enclose maximum volumeBC2 will enclose maximum volumeCC3 will enclose maximum volumeDEach of C1,C2 and C3 will enclose equal volume.
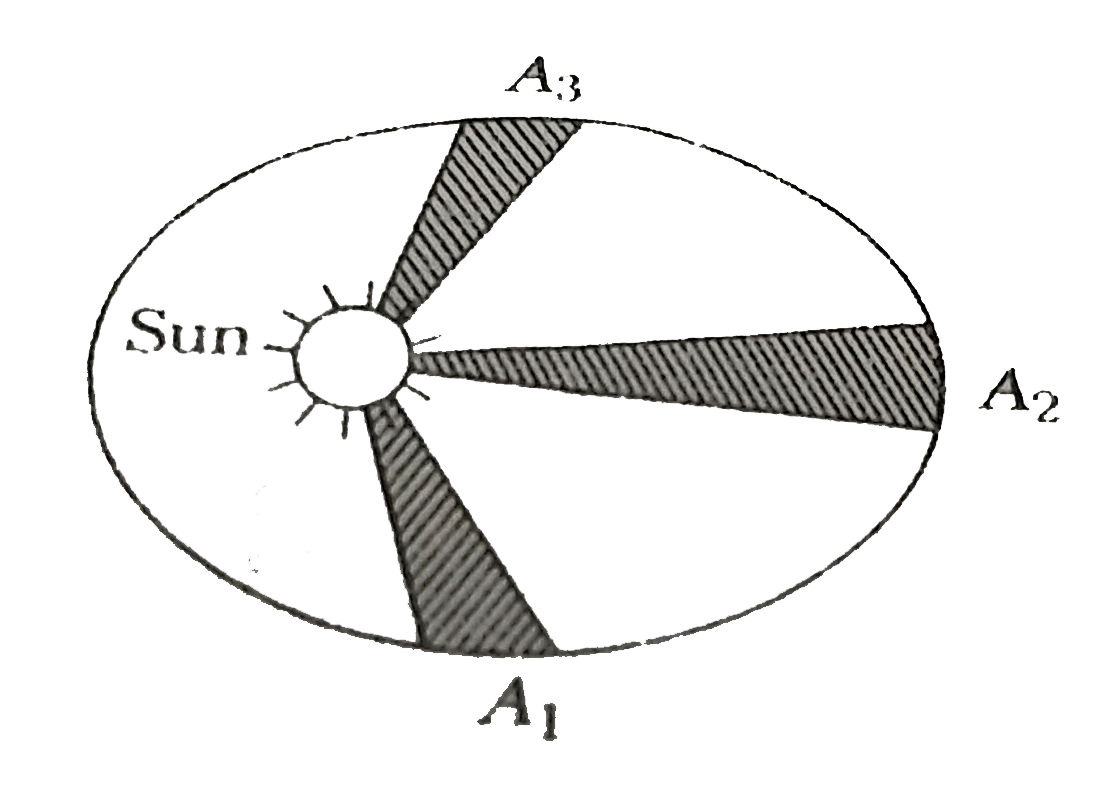
In Fig. the line that join a planet to the sun sweep out areas A1,A2,A3 in time intervals 6 weeks, 3 weeks and 2 weeks respectively. How are A1,A2,A3 ?realted
View SolutionA planet moving around sun sweeps area A1 in 2 days, A2 in 3 days and A3 in 6 days, then find the relation between A1,A2andA3
View SolutionIf an=3−4n, then what is a1+a2+a3+…+an equal to ?
View SolutionIf a1,a2,a3 are the last three digits of 17256 respectively then the value of a2−a1−a3 is equal
View SolutionAn equivalence relation R in A divides it into equivalence classes A1,A2,A3. What is the value of A1∪A2∪A3 and A1∩A2∩A3
View Solution