The magnetic fiedl at the cetre of a circular loop of diameter 0.1 m and carrying a current of 1 A is
2.5×10−5T
1.25×10−5T
3.8×10−5T
4.6×10−5T
The correct Answer is:B
To find the magnetic field at the center of a circular loop carrying a current, we can use the formula:
B=μ0I2R
where:
- B is the magnetic field at the center of the loop,
- μ0 is the permeability of free space, approximately 4π×10−7T m/A,
- I is the current in amperes,
- R is the radius of the loop in meters.
1. Identify the given values:
- Diameter of the loop, d=0.1m
- Current, I=1A
2. Calculate the radius of the loop:
R=d2=0.1m2=0.05m
3. Substitute the values into the formula:
B=μ0I2R=(4π×10−7T m/A)×(1A)2×(0.05m)
4. Calculate the denominator:
2R=2×0.05m=0.1m
5. Calculate the magnetic field:
B=(4π×10−7)0.1=4π×10−6T
6. Approximate the value of B:
B≈4×3.14×10−6T≈12.56×10−6T≈12.56μT
Final Answer:
The magnetic field at the center of the circular loop is approximately 12.56μT.
- B is the magnetic field at the center of the loop,
- μ0 is the permeability of free space, approximately 4π×10−7T m/A,
- I is the current in amperes,
- R is the radius of the loop in meters.
- Diameter of the loop, d=0.1m
- Current, I=1A
R=d2=0.1m2=0.05m
B=μ0I2R=(4π×10−7T m/A)×(1A)2×(0.05m)
2R=2×0.05m=0.1m
B=(4π×10−7)0.1=4π×10−6T
B≈4×3.14×10−6T≈12.56×10−6T≈12.56μT
The magnetic field at the center of the circular loop is approximately 12.56μT.
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - MCQ (HIGHER LEVEL)34videos
MAGNETIC EFFECT OF ELECTRIC CURRENT
- BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - MCQ (GRAPHICAL MCQS)2videos
MAGNETIC EFFECT OF ELECTRIC CURRENT
- BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - MCQ (HIGHER LEVEL)3videos
MAGNETIC EFFECT OF ELECTRIC CURRENT
- BOOK - MARVEL PUBLICATIONCHAPTER - FRICTIONAL IN SOLIDS AND LIQUIDS EXERCISE - TEST YOUR GRASP10videos
FRICTIONAL IN SOLIDS AND LIQUIDS
- BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETISMEXERCISE - TEST YOUR GRASP10videos
MAGNETISM
Similar Questions
A current circular conducting loop exerts a magnetic field both inside and outside it. The magnetic field at the cetre of a current loop of radius 'R' and carrying a current I is given as :
B=μ0I2R
The magnetic field lines due to a circular current loop form closed loops. The direction of the magnetic field is given by the right hand thumb rule, which states that if one curls the palm of his right hand around the current loop with the fingers pointing in the direction of the current, the right hand thumb will give the direction of the magnetic field. From this law it is clear that the direction of magnetic field →B is always perpendicular to the direction of flow of current or perpendicular to the plane of circular current loop.
Draw the magnetic field lines due to a circular current loop placed in a horizontal plane.View SolutionA current circular conducting loop exerts a magnetic field both inside and outside it. The magnetic field at the cetre of a current loop of radius 'R' and carrying a current I is given as :
B=μ0I2R
The magnetic field lines due to a circular current loop form closed loops. The direction of the magnetic field is given by the right hand thumb rule, which states that if one curls the palm of his right hand around the current loop with the fingers pointing in the direction of the current, the right hand thumb will give the direction of the magnetic field. From this law it is clear that the direction of magnetic field →B is always perpendicular to the direction of flow of current or perpendicular to the plane of circular current loop.

How is the magnetic field at O modified when the two loops are rearranged as shown in Fig.View Solution
Knowledge Check
- Question 1 - Select One
Magnetic field intensity H at the centre of a circular loop of radius r carrying current I e.m.u. is
ArI oerstedB2πr oerstedCI2πr oerstedD2πrI oersted - Question 2 - Select One
To produce a magnetic field of π tesla at the centre of circular loop of diameter 1 m, the current flowing through loop is :
A5×106AB107AC2.5×106AD2×106A - Question 3 - Select One
The product a maganetic field of π tesla at the centre of circular loop of diameter 1m the current following through loop is
A5×106AB107AC2.5×106AD2×106A
A current circular conducting loop exerts a magnetic field both inside and outside it. The magnetic field at the cetre of a current loop of radius 'R' and carrying a current I is given as :
B=μ0I2R
The magnetic field lines due to a circular current loop form closed loops. The direction of the magnetic field is given by the right hand thumb rule, which states that if one curls the palm of his right hand around the current loop with the fingers pointing in the direction of the current, the right hand thumb will give the direction of the magnetic field. From this law it is clear that the direction of magnetic field →B is always perpendicular to the direction of flow of current or perpendicular to the plane of circular current loop.
Does a charge at rest produes a magnetic field around it?View SolutionA current circular conducting loop exerts a magnetic field both inside and outside it. The magnetic field at the cetre of a current loop of radius 'R' and carrying a current I is given as :
B=μ0I2R
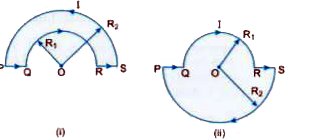
The magnetic field lines due to a circular current loop form closed loops. The direction of the magnetic field is given by the right hand thumb rule, which states that if one curls the palm of his right hand around the current loop with the fingers pointing in the direction of the current, the right hand thumb will give the direction of the magnetic field. From this law it is clear that the direction of magnetic field →B is always perpendicular to the direction of flow of current or perpendicular to the plane of circular current loop.
Determine the magnetic field at the centre point O due to two concentric semicircular loops of radii R1andR2 carrying a current I, when the loops of radii R1andR2 carrying a current I, when the loops are arranged as shown in Fig.View SolutionWhat is the magnetic moment of a circular loop of radius R carrying current I clockwise?
View SolutionMagnetic induction produced at the center of a circular loop of radius R carrying a current is 'B' The magnetic moment of the loop is
View SolutionThe magnetic induction of the centre of circular coil carrying current of 1.4 A is 1.76×10−6 N/A m then the circumference of the loop is
View Solution

