The mass of a 250 cm3 flask is 287 mg more when it is filled with an unknown gas than when it is evacuated. When the flask is filled, the gas is at 20∘C and 1.00×105 Pa. What is the molecular mass of the gas molecules.
To find the molecular mass of the unknown gas, we can use the Ideal Gas Law, which is given by the equation:
PV=nRT
Where:
- P = Pressure (in Pascals)
- V = Volume (in cubic meters)
- n = Number of moles of the gas
- R = Universal gas constant (8.314J/(mol K))
- T = Temperature (in Kelvin)
Step 1: Convert the given volume from cm³ to m³
The volume of the flask is given as 250 cm³. To convert this to cubic meters:
V=250cm3=250×10−6m3=2.5×10−4m3
Step 2: Convert the temperature from Celsius to Kelvin
The temperature is given as 20∘C. To convert this to Kelvin:
T=20+273=293K
Step 3: Identify the mass of the gas
The mass of the gas is given as 287 mg. To convert this to kilograms:
m=287mg=287×10−6kg=2.87×10−4kg
Step 4: Calculate the number of moles of gas
Using the relationship between mass and number of moles, we have:
n=mM
Where M is the molar mass of the gas. Rearranging the Ideal Gas Law gives:
n=PVRT
Substituting for n:
mM=PVRT
Step 5: Rearranging to find the molar mass M
Rearranging the equation to solve for M:
M=mRTPV
Step 6: Substitute the known values into the equation
Now we can substitute the values we have:
- m=2.87×10−4kg
- R=8.314J/(mol K)
- T=293K
- P=1.00×105Pa
- V=2.5×10−4m3
Substituting these values into the equation for M:
M=(2.87×10−4kg)(8.314J/(mol K))(293K)(1.00×105Pa)(2.5×10−4m3)
Step 7: Calculate the value
Calculating the numerator:
Numerator=2.87×10−4×8.314×293≈6.956kg m2/s2(J)
Calculating the denominator:
Denominator=1.00×105×2.5×10−4=25Pa m3
Now substituting these values into the equation for M:
M≈6.95625≈0.27824kg/mol=278.24g/mol
Final Answer
The molecular mass of the gas is approximately 278.24g/mol.
---
- P = Pressure (in Pascals)
- V = Volume (in cubic meters)
- n = Number of moles of the gas
- R = Universal gas constant (8.314J/(mol K))
- T = Temperature (in Kelvin)
The volume of the flask is given as 250 cm³. To convert this to cubic meters:
The temperature is given as 20∘C. To convert this to Kelvin:
The mass of the gas is given as 287 mg. To convert this to kilograms:
Using the relationship between mass and number of moles, we have:
Rearranging the equation to solve for M:
Now we can substitute the values we have:
- R=8.314J/(mol K)
- T=293K
- P=1.00×105Pa
- V=2.5×10−4m3
Calculating the numerator:
The molecular mass of the gas is approximately 278.24g/mol.
Topper's Solved these Questions
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Advance MCQs with One or More Options Correct
15 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO
66 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - U.N.P
79 Videos
Similar Questions
Knowledge Check
An equimolar mixture of Nitrogen gas and water vapours is taken in a 2 litre flask at 27∘C and 1.23×10−2 atm. pressure. What is the mass of the gas at −27∘C?
A2.8×10−4gB5.2×10−3gC1.4×10−2gD0.07gA 2.00 litre evacuated container has a mass of 1050.0g. When the container is filled with an unknown gas at 800mm Hg pressure and 25.0∘C the mass is 1052.4g. What is the molar mass of the gas (in gmol−1)?
A28B31C54D56If the density of a gas A is 1.5 times that of B, then the molecular mass of A is M. The molecular mass of B will be
A1.5MBM/1.5C3MDM/3
The density of an ideal gas is 1.25×10−3gcm−3 at STP. Calculate the molecular weight of the gas.
View SolutionThe density of an unknown gas at 98∘C and 0.974atm is 2.5×10−3g/ml. What is the mol.wt. of gas ?
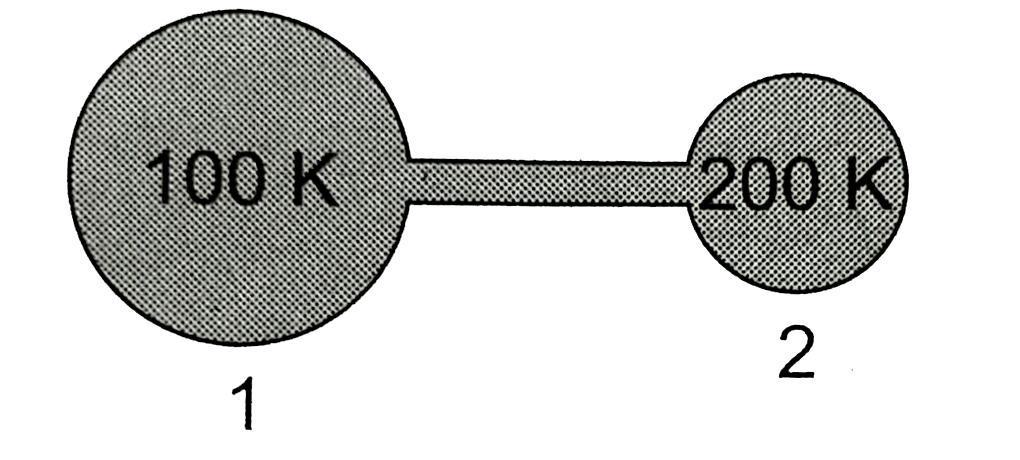
View SolutionThe given figure shows two flasks connected to each other. The volumo of flask 1 is twice that of flask 2 . The system is filled with an ideal gas at temperatare 100K and 200K respectively, in the flasks. If the mass of the gas in flask 1 be m, then the mass of the gas in flesk 2 in equilibriam is (mx). Find x.
'(##CEN_KSR_PHY_JEE_C13_E01_004_Q01##)'
View Solution1.40L of an unknown gas requires 57 second to diffuse and the same volume of N2 gas takes 84 second to diffuse at the same temperature and pressure. What is the molecular mass of the unknown gas?
View SolutionFigure shows two flasks connected to each other. The volume of the flask 1 is twice that of flask 2. The system is filled with an ideal gas at temperature 100K and 200K respectively. If the mass of the gas in 1 be m then what is the mass of the gas in flask 2
View Solution
