The masses and radii of the earth an moon are M1andR1andM2,R2 respectively. Their centres are at a distacne r apart. Find the minimum speed with which the particle of mass m should be projected from a point mid-way between the two centres so as to escape to infinity.
2[G(M1+M2)md]1/2
2[G(M1+M2)d]1/2
2[2(M1−M2)md]1/2
2[G(M1−M2)d]1/2
The correct Answer is:b
The potential energy of particle P due to earth is
−GmM1r=−GmM1d/2=−2GM1md
P.E. due to moon at p is −2GM2md
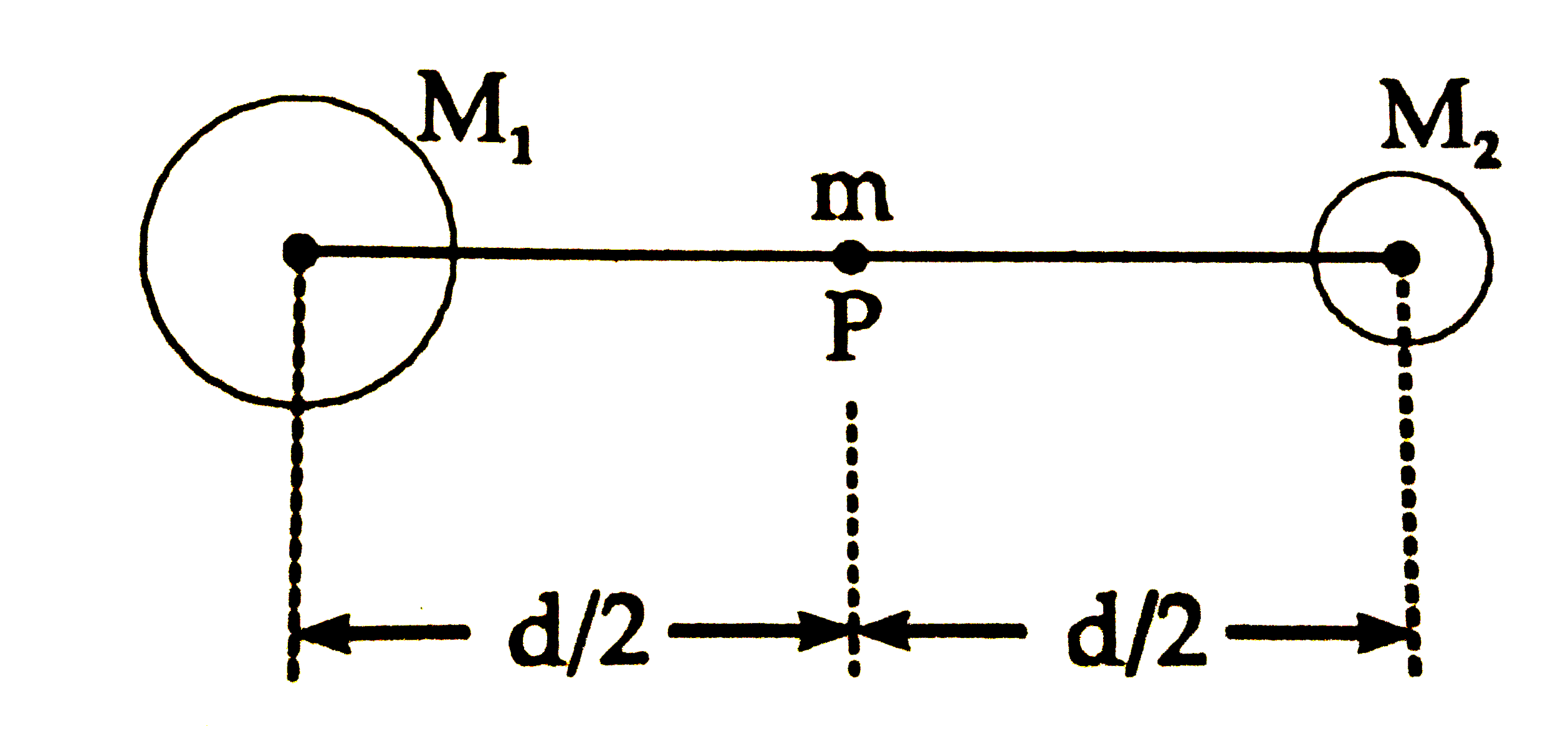
∴ Total potential energy =−2Gmd(M1+M2)
If the particle P is projected with a velocity v, its kinetic energy =1/2mv2.
Therefore, the total initial energy of the particle is
E1=−2Gmd(M1+M2)+12mv2.
If the particle is to escape to infinity, its final potential and kinetic energy will be zero. Thus the total energy Ef=0.
From the principle of conservation of energy,
E1=Ef=−2Gmd(M1+M2)+12mv2=0
Which gives.
v=2[G(M1+M2)d]1/2
Topper's Solved these Questions
Similar Questions
The masses and radii of the Earth and the Moon are M1,R1andM2,R2 respectively. Their centres are at a distance d apart. The minimum speed with which a particel of mass m should be projected from a point midway between the two centres so as to escape to infinity is ........
View SolutionThe masses and radii of the earth and moon are (M1,R1) and (M2,R2) respectively. Their centres are at a distance r apart. Find the minimum escape velocity for a particle of mass 'm' to be projected from the middle of these two masses :
View Solution
Knowledge Check
The radii of a planet and its satellite are 2r and r and their densities are ρ and 2ρ respectively. Their centres are separated by a distance d. The minimum speed with which a body should be projected from the mid point of the line joining their centres so that the body escapes to infinity is (G-universal gravitational constant)
A4⎡⎣√10Gπr3ρ3d⎤⎦B√40Gπr3ρ3d⎤⎦C2⎡⎣√10Gπr3ρd⎤⎦D14⎡⎣√10Gπr3ρ3d⎤⎦Two racing cars having masse m1andm2 move in concentric circle of radii r1andr2 respectively. If their angular speed are same , then ratio of their linear speed is
Am1:m2Br1:r2C1:1Dm1r1:m2r2Two satellite fo masses m and 4m orbit the earth in circular orbits of radii 4r and r respectively. The ratio of their orbital speed is
A1B12C1√2D1√5
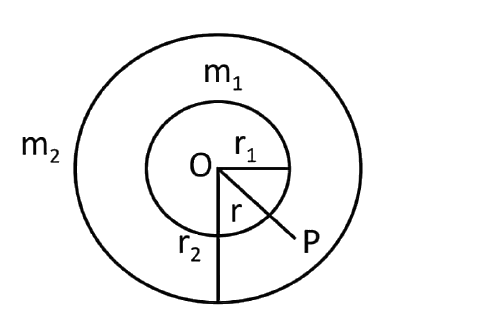
Two concentric spherical shells of masses and radii m1,r1andm2,r2 respectively are as shown. The gravitational field intensity at point P is
View SolutionEarth and moon centre distance is 'r'. From the mid point what should be the speed of the particle so that it can escape to infinity?
View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.

View SolutionTwo satellites of masses 3 m and m orbit the earth in circular orbits of radii r and 3 r respectively. The ratio of the their speeds is
View SolutionIf d is the distance between the centre of the earth of mass M1 and the moon of mass M2, then the velocity with which a body should be projected from the mid point of the line joining the earth and the moon, so that it just escape is
View Solution
