The masses in figure slide on a frictionless table. m1 but not m2, is fastened to the spring. If now m1 and m2 are pushed to the left , so that the spring is compressed a distance d, what will be the amplitude of the oscillation of m1 after the spring system is released ?

The correct Answer is:A, B, D
While returning to equilibrium position,
12kd2=12(m1+m2)v2
∴v=(√k1m1+m2)d
Now, after mean position m2 is detached from m1 and keeps on moving with this constant velocity v towards right. Block m1 starts SHM with spring and this v becomes its maximum velocity at mean position.
∴v=ωA
∴(√km1+m2)d=(√km1)A
∴A=(√m1m1+m2)d.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Two blocks of masses m1 and m2 are kept on a smooth horizontal table as shown in figure. Block of mass m1 (but not m2 is fastened to the spring. If now both the blocks are pushed to the left so that the spring is compressed a distance d. The amplitude of oscillatin of block of mass m1 after the system is released is
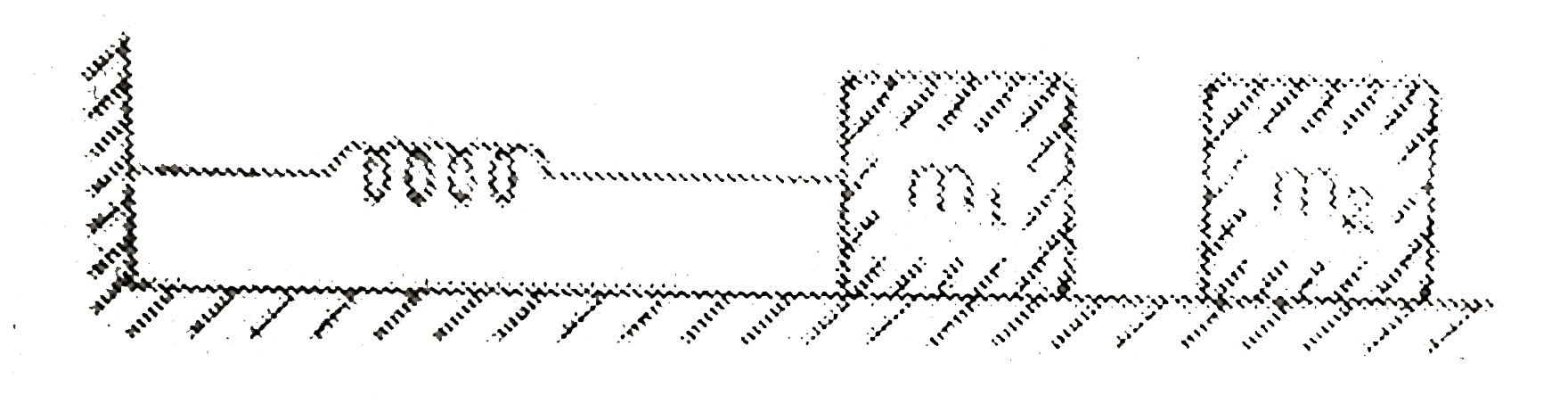
View SolutionThe two masses m1 and m2 are joined by a spring as shown. The system is dropped to the ground from a height. The spring will be

View Solution
Knowledge Check
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
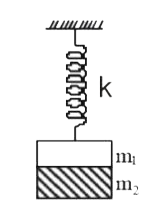
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)mTwo masses m1andm2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Then the angular frequency of oscillation of m2 is
A√(k/m1)B√(k/m2)C√[k(m1+m2)]D√[k/(m1m2)]
Two masses m and 2m are attached to two ends of an ideal spring as shown in figure. When the spring is in the compressed state, the energy of the spring is 60 J, if the spring is released, then at its natural length

View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View SolutionTwo masses m1 and m2 are suspended together by a massless spring of constant K. When the masses are in equilibrium, m1 is removed without disturbing the system. Then the angular frequency of oscillation of m2 is -
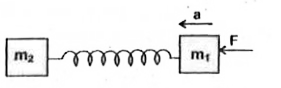
View SolutionTwo blocks of masses m1 and m2 are connected to each other with the help of a spring. If pushing force F is given to the mass m1 providing acceleration a to it, then acceleration of m2 is
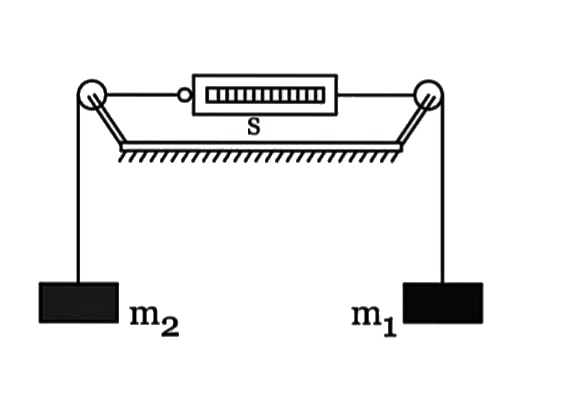
View SolutionIn the arrangement shown, the pulleys, string and the spring balance, all the ideal. If m1>m2, then the reading of the spring balance is
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View Solution
