The maximum speed of a particle in SHM is given by mA=Vm. The average speed of the particle in terms of maximum speed is given by
Vm2
πVm2
2Vmπ
π2Vm
The correct Answer is:C
To find the average speed of a particle in Simple Harmonic Motion (SHM) in terms of its maximum speed, we can follow these steps:
Step 1: Understand the Maximum Speed
The maximum speed Vmax of a particle in SHM is given by the formula:
Vmax=ωA
where ω is the angular frequency and A is the amplitude of the motion.
Step 2: Calculate the Total Distance Covered in One Cycle
In one complete cycle of SHM, the particle moves from the mean position to the maximum amplitude in one direction, back to the mean position, and then to the maximum amplitude in the opposite direction, and back again to the mean position. Therefore, the total distance covered in one cycle is:
Total Distance=4A
Step 3: Determine the Time Period
The time taken to complete one full cycle is known as the time period T. The time period can be expressed in terms of angular frequency as:
T=2πω
Step 4: Relate Angular Frequency to Maximum Speed
From the maximum speed formula, we can express ω in terms of Vmax:
ω=VmaxA
Step 5: Substitute ω into the Time Period Formula
Substituting the expression for ω into the time period formula gives:
T=2πVmaxA=2πAVmax
Step 6: Calculate the Average Speed
The average speed Vavg is defined as the total distance covered divided by the time taken to cover that distance:
Vavg=Total DistanceT=4AT
Substituting the expression for T:
Vavg=4A2πAVmax
Step 7: Simplify the Expression
Now, simplify the expression for average speed:
Vavg=4A⋅Vmax2πA=4Vmax2π=2Vmaxπ
Final Answer
Thus, the average speed of the particle in terms of maximum speed is:
Vavg=2Vmaxπ
---
The maximum speed Vmax of a particle in SHM is given by the formula:
Vmax=ωA
where ω is the angular frequency and A is the amplitude of the motion.
In one complete cycle of SHM, the particle moves from the mean position to the maximum amplitude in one direction, back to the mean position, and then to the maximum amplitude in the opposite direction, and back again to the mean position. Therefore, the total distance covered in one cycle is:
Total Distance=4A
The time taken to complete one full cycle is known as the time period T. The time period can be expressed in terms of angular frequency as:
T=2πω
From the maximum speed formula, we can express ω in terms of Vmax:
ω=VmaxA
Substituting the expression for ω into the time period formula gives:
T=2πVmaxA=2πAVmax
The average speed Vavg is defined as the total distance covered divided by the time taken to cover that distance:
Vavg=Total DistanceT=4AT
Substituting the expression for T:
Vavg=4A2πAVmax
Now, simplify the expression for average speed:
Vavg=4A⋅Vmax2πA=4Vmax2π=2Vmaxπ
Thus, the average speed of the particle in terms of maximum speed is:
Vavg=2Vmaxπ
Topper's Solved these Questions
Similar Questions
The x-t graph of a particle executing S.H.M. is given as then maximum accleration of the particle is given as :-
View SolutionThe figure shows the force (F) versus displacement (s) graph for a particle of mass m=2kg initially at rest.
(i) The maximum speed of the particle occurs at x = …..m
(ii) The maximum speed of the particle is ….ms−1
(iii) The particle once again has its speed zero at x =....m
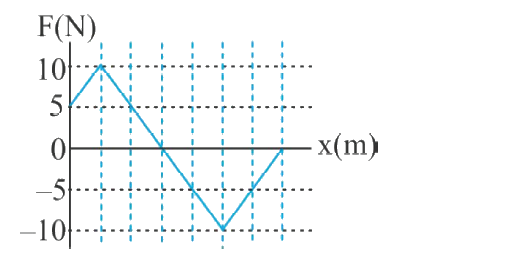
View Solution
Knowledge Check
Maximum speed of a particle in simple harmonic motion is vmax. Then average speed of this particle in one time period is equal to
Avmax2BvmaxπCπvmax2D2vmaxπThe displacement of a particle executing SHM is given by y=0.5 sint cm . The maximum speed of the particle is
A200 cms−1B100 cms−1C50 cms−1D5.25 cms−1Maximum speed of a particle in simple haromonic motion is vmax. Then average speed of a particle in one complete oscillation is equal to
Avmax2BvmaxπCπvmax2D2vmaxπ
The displacement of a particle executing S.H.M. is given by y = 0.25 sin 200t cm. The maximum speed of the particle is
View SolutionThe displacement of a particle executing S.H.M. is given by, y = 0.20 sin (100 t) cm. The maximum speed of the particle is
View SolutionIf the maximum speed of a particle on a travelling wave is v0, then find the speed of a particle when the displacement is half of the maximum value.
View SolutionIf speed of a particle is given by v=ACsin(At+B), the dimension of C is
View SolutionThe ratio of instantaneous velocity and the average speed of the particle performing S.H.M. is
View Solution
