The minimum number of condensers each capacitance of 2μF, in order to obtain result capacitance of 5μF will be
4
5
6
3
The correct Answer is:A
To solve the problem of finding the minimum number of capacitors, each with a capacitance of 2μF, required to achieve a resultant capacitance of 5μF, we can follow these steps:
Step 1: Understand the Capacitor Combinations
We can combine capacitors in two ways: in series and in parallel. The total capacitance for capacitors in series is given by:
1Ctotal=1C1+1C2+…
For capacitors in parallel, the total capacitance is simply the sum of the individual capacitances:
Ctotal=C1+C2+…
Step 2: Calculate the Capacitance in Series
To achieve a capacitance of 5μF, we can first consider creating a smaller capacitance using the series combination. If we connect two 2μF capacitors in series:
1Cseries=12+12=11⇒Cseries=1μF
Step 3: Create the Required Capacitance
Now, we need to achieve 5μF. We can do this by combining the 1μF capacitor (from the series combination) with other 2μF capacitors in parallel.
If we connect two 2μF capacitors in parallel:
Cparallel=2+2=4μF
Now, we can combine the 1μF capacitor (from the series combination) with the 4μF capacitor (from the parallel combination):
Ctotal=1+4=5μF
Step 4: Count the Total Number of Capacitors Used
- For the series combination: We used 2 capacitors to create 1μF.
- For the parallel combination: We used 2 capacitors to create 4μF.
Thus, the total number of capacitors used is:
2+2=4
Conclusion
The minimum number of 2μF capacitors required to achieve a resultant capacitance of 5μF is 4 capacitors.
We can combine capacitors in two ways: in series and in parallel. The total capacitance for capacitors in series is given by:
1Ctotal=1C1+1C2+…
For capacitors in parallel, the total capacitance is simply the sum of the individual capacitances:
Ctotal=C1+C2+…
To achieve a capacitance of 5μF, we can first consider creating a smaller capacitance using the series combination. If we connect two 2μF capacitors in series:
1Cseries=12+12=11⇒Cseries=1μF
Now, we need to achieve 5μF. We can do this by combining the 1μF capacitor (from the series combination) with other 2μF capacitors in parallel.
Cparallel=2+2=4μF
Ctotal=1+4=5μF
- For the series combination: We used 2 capacitors to create 1μF.
- For the parallel combination: We used 2 capacitors to create 4μF.
2+2=4
The minimum number of 2μF capacitors required to achieve a resultant capacitance of 5μF is 4 capacitors.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced
44 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
Knowledge Check
Minimum number of capacitors each of 8μF and 250 V used to make a composite capacitor of 16μF and 1000 V are
A8B32C16D24Three capacitors each of capacity 4μF are to be connected in such a way that the effective capacitance is 6μF. This can be done by
Aconnecting them in seriesBconnecting them is parallelCconnecting two in series and one in parallelDconnecting two in parallel and one is series
Seven capacitors each of capacitance 2μF are to be connected in a configuration to obtain an effective capacitance of (1011)μF. Which of the combination (s) shown in figure will achieve the desired result?
View SolutionThe effective capacitence in μF in between A and B will be
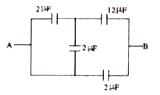
View SolutionA spherical drop of capacitance 12μF is broken into eight drops of equal radius. What is the capacitance of each small drop in μF?
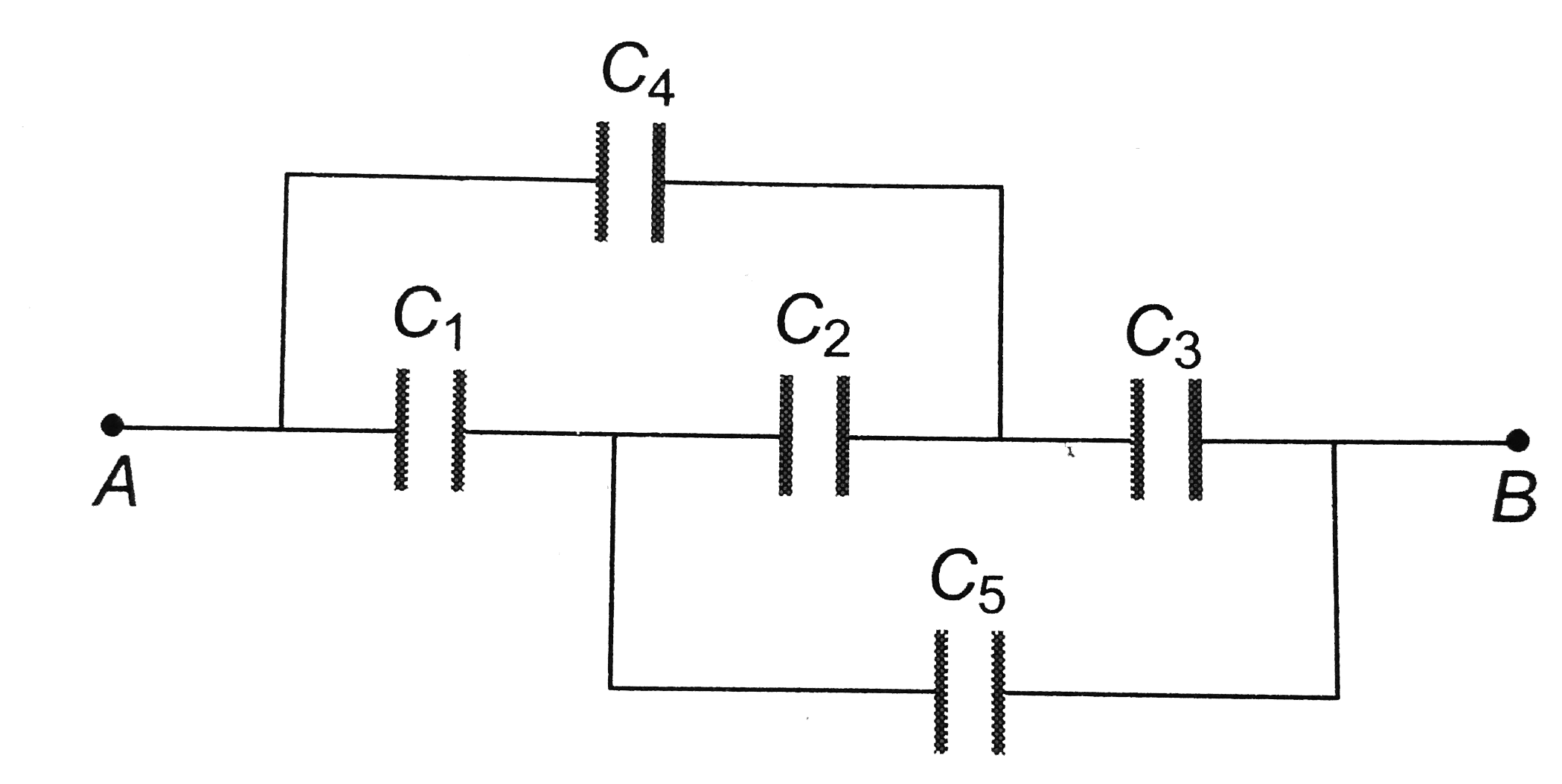
View SolutionIn the given figure the capacitors C1,C3,C4,C5 have a capaciance 4μF each if the capaitor C2 has a capacitance 10μF, then effective capacitance between A and B will be
View SolutionThree capacitors each of capacity 4μF are to be connected in such a way that the effective capacitance is 6μF. This can be done by
View SolutionThree capacitors each of capacity 4μF are to be connected in such a way that the effective capacitance is 6μF. This can be done by
View Solution
