The mixture of a pure liquid and a solution in a along vertical column (i.e., horizontal dimensions << vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical is deviated from its original path. Find the deviation in travelling a horizontal distance d<<h, the height of the column.
The correct Answer is:D
Let us consider a light ray entering the column at (x,y) at 90∘ to the vertical . θ be the angle of incidence at x and it enetr the thin coloum at height y.dθ is the deviation of ray betweem x and (x+dx) emerging at (x+dx,y+dy) at angle (θ+dθ).

By snell's law,
μ(y)sinθ=μ(y+dy)sin(θ+dθ)
[μ(y)+dμdydy](sinθcosdθ+cosθsindθ)
As dθ is small, cosdθ≈1 and sindθ≈dθ.
∴μ(y)cosθ=dμdydysinθ,dθ=−1μdμdytanθdy
[tanθ=dxdy and replacing μ(y) by μ]
θ=−1μdμdyd∫odx=−1μ(dμdy)d.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT EXAMPLAR PROBLEMS11videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSERTION AND REASON15videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 350videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason15videos
SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS
Similar Questions
Knowledge Check
- Question 1 - Select One
A right-angled prism of apex angle 4∘ and refractive index 1.5 is located in front of a vertical plane mirror as shown in figure. A horizontal ray of light is falling on the prism. Find the total deviation produced in the light ray as it emerges 2nd time from the prism.
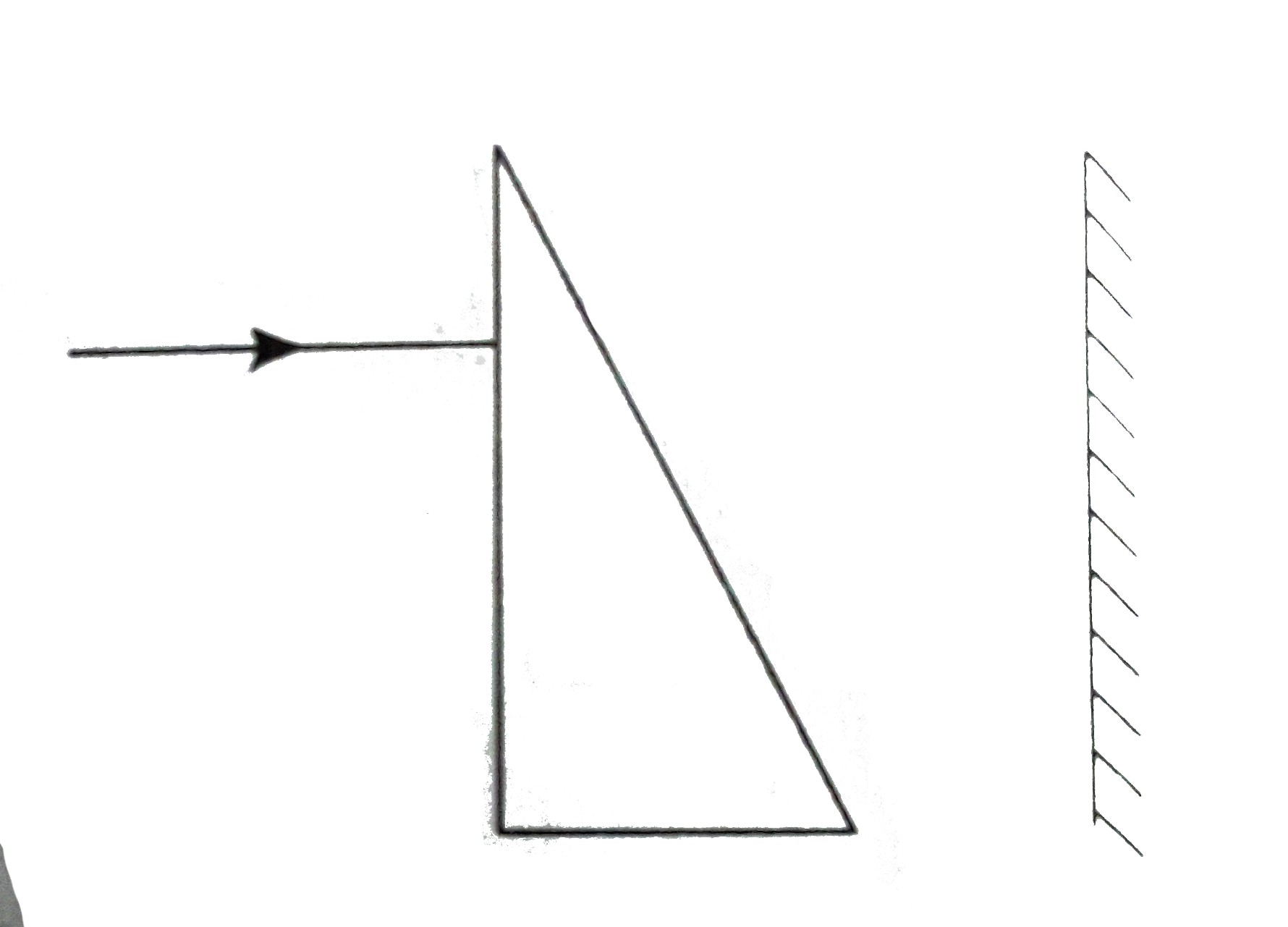 A8∘CWB6∘CWC180∘CWD174∘CW
A8∘CWB6∘CWC180∘CWD174∘CW - Question 2 - Select One
A prism having an apex angle of 4∘ and refractive index of 1.50 is located in front of a vertical plane mirror as shown in the figure. A horizontal ray of light is incident on the prism. The total angle through which the ray is deviated is:
 A4∘ clockwiseB178∘ clockwiseC2∘ clockwiseD8∘ clockwise
A4∘ clockwiseB178∘ clockwiseC2∘ clockwiseD8∘ clockwise
A force of 4N is inclined at an angle of 60∘ from the vertical. Find out its components along horizontal and vertical directions.
 View Solution
View SolutionA force of 4N is inclined at an angle of 60∘ from the vertical. Find out its components along horizontal and vertical directions.
 View Solution
View SolutionThe tabular arrangment of elements in horizontal rows and vertical columns……………….
View SolutionA right-angled prism of apex angle 4∘ and refractive index 1.5 is located in front of a vertical plane mirror as shown in figure. A horizontal ray of light is falling on the prism. Find the total deviation produced in the light ray as it emerges 2nd time from the prism.
 View Solution
View SolutionA prism having an apex angle of 4∘ and refractive index of 1.50 is located in front of a vertical plane mirror as shown in the figure. A horizontal ray of light is incident on the prism. The total angle through which the ray is deviated is:
 View Solution
View SolutionTwo vertical plane mirrors are inclined at an angle of 60∘ with each other. A ray of light travelling horizontally is reflected first from one mirror and then from the other. The resultant deviation is
View Solution

