The molar heat capacity in a process of a diatomic gas if it does a work of Q4 when a heat of Q is supplied to it is
25R
52R
103R
67R
The correct Answer is:C
To solve the problem, we need to determine the molar heat capacity C of a diatomic gas given that it does work W=Q4 when a heat Q is supplied to it.
1. Understand the First Law of Thermodynamics:
The first law of thermodynamics states that:
ΔU=Q−W
where ΔU is the change in internal energy, Q is the heat added to the system, and W is the work done by the system.
2. Substitute the Given Values:
From the problem, we know:
W=Q4
Therefore, substituting this into the first law gives:
ΔU=Q−Q4=Q(1−14)=Q(34)=3Q4
3. Relate Change in Internal Energy to Temperature Change:
For a diatomic gas, the change in internal energy can also be expressed as:
ΔU=nCVΔT
where CV is the molar heat capacity at constant volume. For a diatomic gas, CV=52R.
4. Express ΔT:
We can equate the two expressions for ΔU:
nCVΔT=3Q4
Substituting CV:
n(52R)ΔT=3Q4
5. Solve for ΔT:
Rearranging gives:
ΔT=3Q4⋅25nR=3Q10nR
6. Calculate Molar Heat Capacity C:
Molar heat capacity C is defined as:
C=QΔT
Substituting for ΔT:
C=Q3Q10nR=Q⋅10nR3Q=10nR3
7. Final Expression for Molar Heat Capacity:
Since we are looking for the molar heat capacity per mole, we can express it as:
C=103R
Conclusion:
The molar heat capacity of the diatomic gas in this process is:
C=103R
The first law of thermodynamics states that:
ΔU=Q−W
where ΔU is the change in internal energy, Q is the heat added to the system, and W is the work done by the system.
From the problem, we know:
W=Q4
Therefore, substituting this into the first law gives:
ΔU=Q−Q4=Q(1−14)=Q(34)=3Q4
For a diatomic gas, the change in internal energy can also be expressed as:
ΔU=nCVΔT
where CV is the molar heat capacity at constant volume. For a diatomic gas, CV=52R.
We can equate the two expressions for ΔU:
nCVΔT=3Q4
Substituting CV:
n(52R)ΔT=3Q4
Rearranging gives:
ΔT=3Q4⋅25nR=3Q10nR
Molar heat capacity C is defined as:
C=QΔT
Substituting for ΔT:
C=Q3Q10nR=Q⋅10nR3Q=10nR3
Since we are looking for the molar heat capacity per mole, we can express it as:
C=103R
The molar heat capacity of the diatomic gas in this process is:
C=103R
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Application Of First Law Of Thermodynamics In Different Situations25videos
KINETIC THEORY OF GASES AND THERMODYNAMICS
- BOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Second Law Of Thermodynamics29videos
KINETIC THEORY OF GASES AND THERMODYNAMICS
- BOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Ideal Gas Equation32videos
KINETIC THEORY OF GASES AND THERMODYNAMICS
- BOOK - A2ZCHAPTER - GRAVITATIONEXERCISE - Chapter Test29videos
GRAVITATION
- BOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration15videos
MOCK TEST
Similar Questions
Knowledge Check
- Question 1 - Select One
The molar heat capacity of a gas in a process
Ais either CVorCPBlies between CVorCPCmay range from zero to infinityDcan have any real value - Question 2 - Select One
Molar heat capacity of a gas is
AExtensive propertyBIntensive propertyCChemical property of gasDColligative property - Question 3 - Select One
The molar heat capacity for the process shown in fig. is
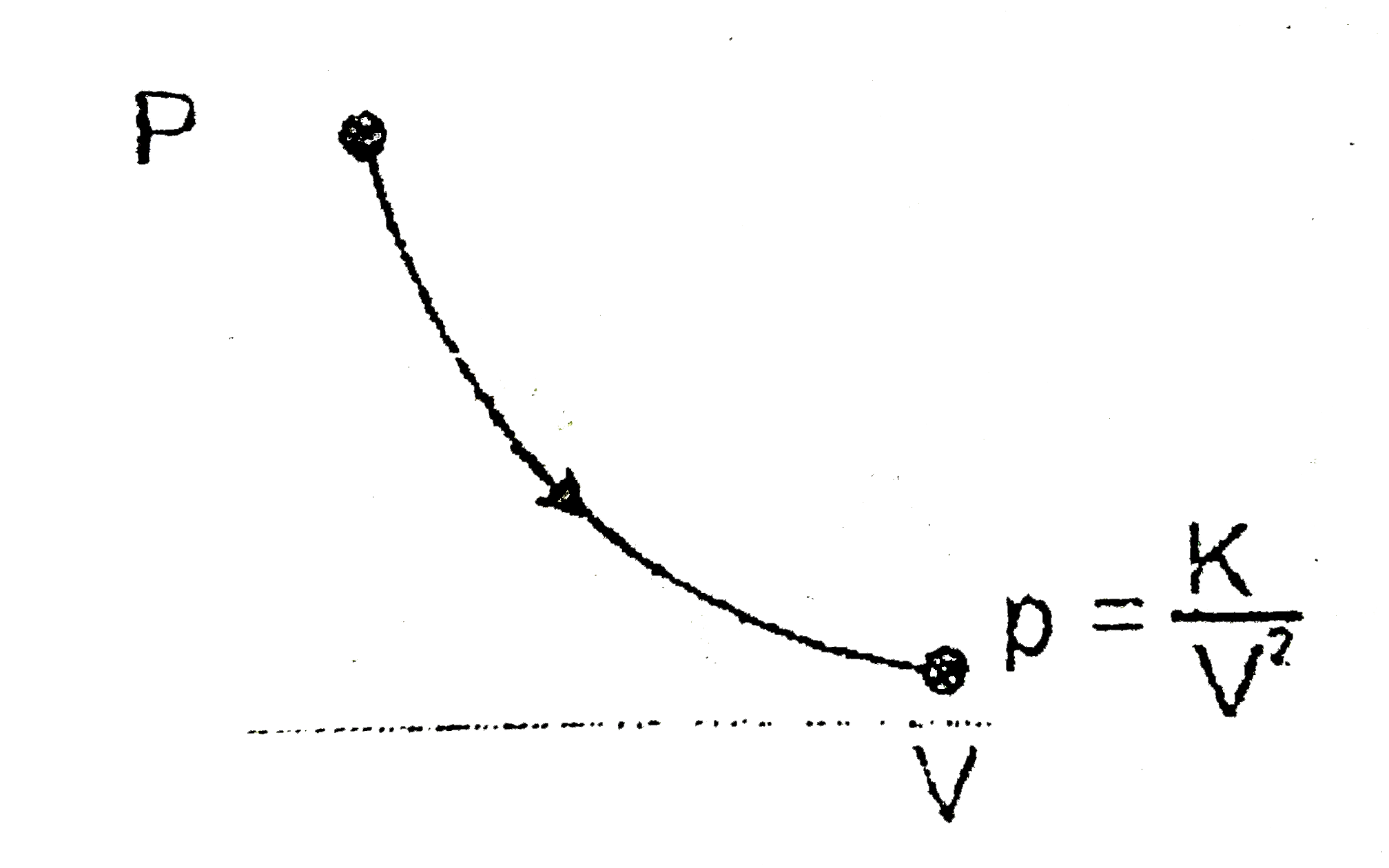 AC=CvBC=CpCC>CvDC<Cv
AC=CvBC=CpCC>CvDC<Cv
The heat capacity of a diatomic gas is higher than that of a monatomic gas.
View SolutionThe molar heat capacity for the process shown in fig. is
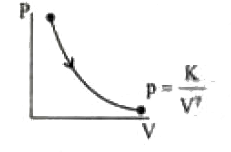 View Solution
View SolutionThe molar heat capacity for the process shown in figure is
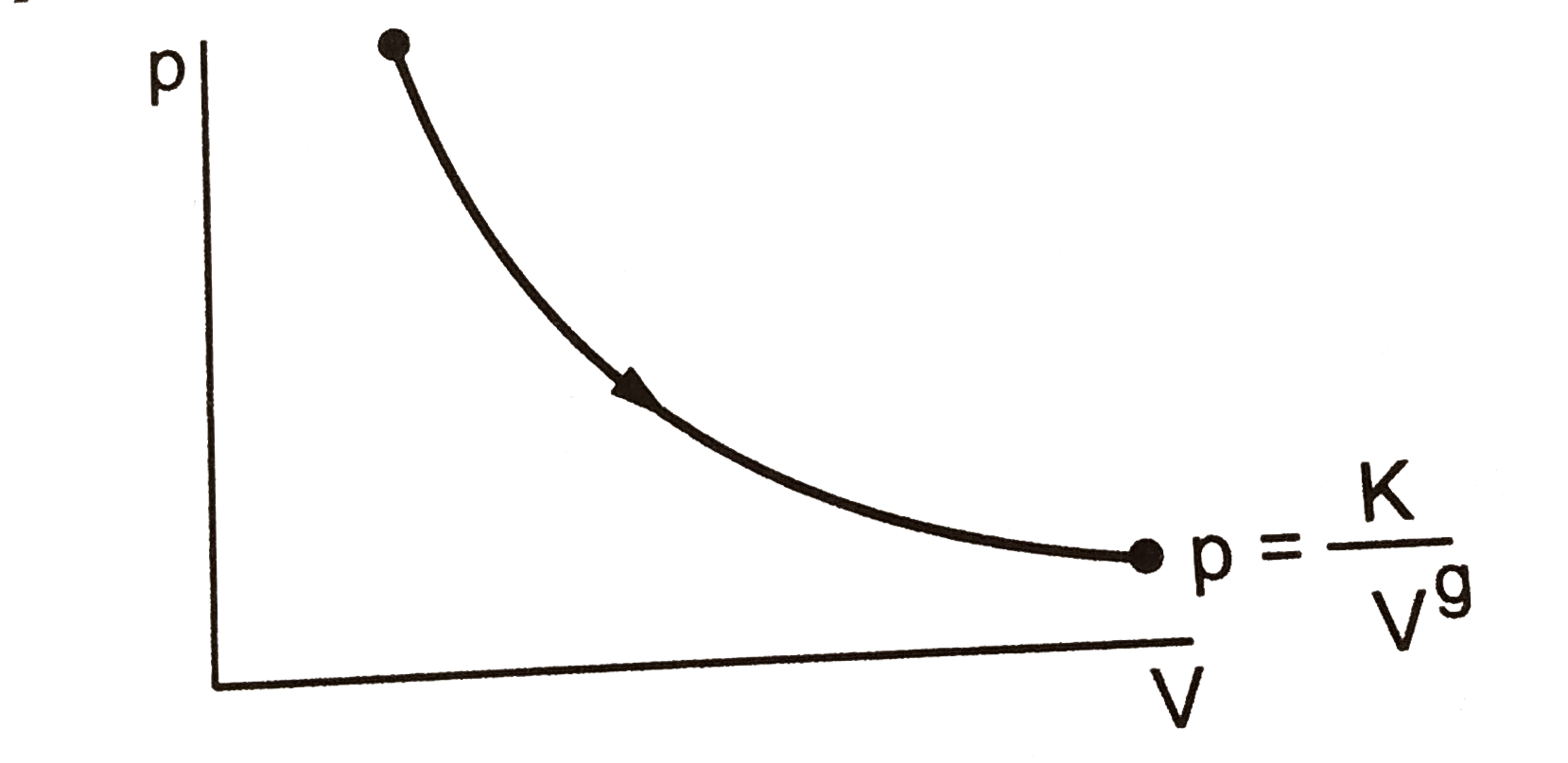 View Solution
View SolutionThe molar heat capacity for a gas at constant T and P is
View SolutionIn a process, the molar heat capacity of a diatomic gas is 103R. When heat Q is supplied to the gas, find the work done by the gas
View Solution

