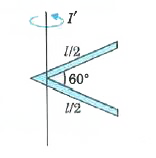
The moment of inertia of a rod about an axis through its centre and perpendicular to it, is $\frac{1}{12} M L^{2}$ (where, M is the mass and L is length of the rod). The rod is bent in the middle, so that two halves make an angle of $60^{\circ}$ . The moment of inertia of the bent rod about the same axis would be

A

$\frac{1}{48} M l^{2}$

B

$\frac{1}{12} M l^{2}$

C

$\frac{1}{24} M l^{2}$

D

$\frac{M l^{2}}{8 \sqrt{3}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Given M.I. of rod about its centre of mass and perpendicular to it is
$I = \frac{1}{12} M l^{2}$
Let l. = moment of inertia of bent rod
$I . = \frac{1}{3} \frac{M}{2} {(\frac{l}{2})}^{2} + \frac{1}{3} \frac{M}{2} {(\frac{l}{2})}^{2}$
$= \frac{1}{12} (\frac{M}{2} l^{2}) + \frac{1}{12} (\frac{M}{2} l^{2})$
$= \frac{2}{12} M l^{2} (\frac{1}{2})$
$= \frac{1}{12} M l^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The moment of inertia of a rod about an axis through its centre and perpendicular to it is $\frac{1}{12} M L^{2}$ (where, M is the mass and L is the length of the rod). The rod is bent in the middle so that the two halves make an angle of $60^{\circ}$ The moment of inertia of the bent rod about the same axis would be :
A $\frac{1}{48} M L^{2}$
B $\frac{1}{12} M L^{2}$
C $\frac{1}{24} M L^{2}$
D $(M L^{2}) ? (8 \sqrt{3})$
Question 2 - Select One
The moment of inertia of a rod about an axis through its centre and perpendicular to it is $\frac{1}{12} M L^{2}$ (where, M is the mass and L is the length of the rod). The rod is bent in the middle so that the two halves make an angle of $60^{\circ}$ The moment of inertia of the bent rod about the same axis would be :
A $\frac{1}{48} M L^{2}$
B $\frac{1}{12} M L^{2}$
C $\frac{1}{24} M L^{2}$
D $(M L^{2}) ? (8 \sqrt{3})$
Question 3 - Select One
The moment of inertia of a rod about an axis passing through its centre and perpendicular to it is $\frac{1}{12} M L^{2}$ (where, M is the mass and L the length of the rod.) The rod is bent in the middle so that the two halves make an angle of $30^{\circ}$ . The moment of inertia of the bent rod about the same axis would be
A $\frac{1}{48} M L^{2}$
B $\frac{1}{12} M L^{2}$
C $\frac{1}{24} M L^{2}$
D $\frac{M L^{2}}{8 \sqrt{3}}$

MODERN PUBLICATION-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) )

Home
Ask Doubt
Profile