The net force versus time graph of a rocket is shown in figure The mass of the rocket is 1200kg. Calculate velocity of rocket, 16 seconds after starting from rest. Neglect gravity.

The correct Answer is:B
Impulse=area under F−t graph
=Δp=m(vf−vi)
∴vf=Aream (as vi=0)
=12×(20×103)(8+16)12000
=200m/s
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.6
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Assertion and Reason
15 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.4
4 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
If the maximum possible exhaust velocity of a rocket be 2km/s calculate the ratio m0/m for it to acquire a veocity of 11.2km/s after starting from rest .
View SolutionA rocket motor consumes 100 kg of fuel per second exhausting it with a speed of 6×103ms−1 What thrust is exerted on the rocket ? What will be the velocity of the rocket at the instant its mass is reduced to (1/40) of its initial mass ? Take initial velocity of rocket as zero . Neglect gravity .
View Solution
Knowledge Check
The velocity time graph of a linear motion is shown in the figure. The distance from the starting point after 8 seconds will be
 .A18 mB6 mC8 mDnone of these
.A18 mB6 mC8 mDnone of theseVelocity time graph of an object of mass 2kg is shown in figure. The force required to move the object for first four seconds is
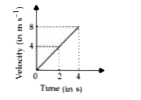 A0NB4NC2ND8N
A0NB4NC2ND8NA rocket is fired upwards. Its velocity versus time graph is shown in the figure-1.131. The maximum height reached by the rocket is:
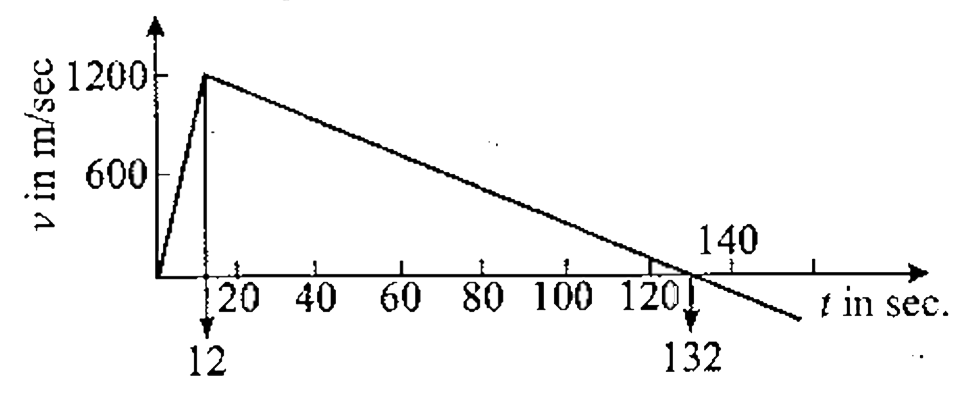 A7.1 kmB79.2 kmC72 kmDInfinite
A7.1 kmB79.2 kmC72 kmDInfinite
The velocity v of mass m of a rocket at time t is given by the equation :
mdvdt+Vdmdt=0,
where 'V' is the constant velocity of emission. If the rocket starts from rest when t=0 with mass m, prove that :
v=Vlog(m0m).
View SolutionCalculate the ratio m0/m for a rocket to attain the escape velocity of 11.2kms−1 after starting from rest, when maximum exhaust velocity of gases is 1.6km/s .
View SolutionA graph of acceleration versus time of a particle starting from rest at t =0 is shown. The speed of the particle at t=14 second is
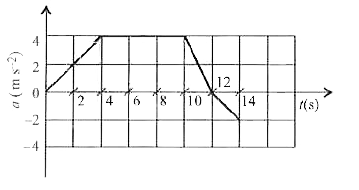
View SolutionIn a rocket, fuel burns at the rate of 2 kg/s. This fuel gets ejected from the rocket with a velocity of 80 km/s. Force exerted on the rocket is -
View SolutionFor a Rocket propulsion velocity of exhaust gases relative to rocket is 2km/s. If mass of rocket system is 1000 kg, then the rate of fuel consumption for a rockt to rise up with acceleration 4.9m/s2 will be:-
View Solution
