The number of atoms of a radioactive substance of half-life T is at t = 0. The time necessary to decay from atoms to atoms will be
T 1n 5
The correct Answer is:C
To solve the problem of determining the time necessary for a radioactive substance to decay from N02 atoms to N010 atoms, we can follow these steps:
1. Understand the decay law: The number of atoms remaining at time t is given by the equation:
Nt=N0e−λt
where Nt is the number of atoms at time t, N0 is the initial number of atoms, and λ is the decay constant.
2. Determine the time t1 for decay to N02:
- Set Nt=N02:
N02=N0e−λt1
- Dividing both sides by N0:
12=e−λt1
- Taking the natural logarithm of both sides:
ln(12)=−λt1
- Therefore, we have:
t1=ln2λ
3. Determine the time t2 for decay to N010:
- Set Nt=N010:
N010=N0e−λt2
- Dividing both sides by N0:
110=e−λt2
- Taking the natural logarithm of both sides:
ln(110)=−λt2
- Therefore, we have:
t2=ln10λ
4. Calculate the time difference t2−t1:
- Now we find the time necessary to decay from N02 to N010:
t2−t1=ln10λ−ln2λ
- Factoring out 1λ:
t2−t1=1λ(ln10−ln2)
- Using the property of logarithms lna−lnb=ln(ab):
t2−t1=1λln(102)=1λln5
5. Relate λ to half-life T:
- The half-life T is given by:
T=ln2λ⟹λ=ln2T
- Substituting λ into the equation for t2−t1:
t2−t1=Tln2ln5
Final Answer:
Thus, the time necessary to decay from N02 atoms to N010 atoms is:
t2−t1=Tln5ln2
Nt=N0e−λt
where Nt is the number of atoms at time t, N0 is the initial number of atoms, and λ is the decay constant.
- Set Nt=N02:
N02=N0e−λt1
- Dividing both sides by N0:
12=e−λt1
- Taking the natural logarithm of both sides:
ln(12)=−λt1
- Therefore, we have:
t1=ln2λ
- Set Nt=N010:
N010=N0e−λt2
- Dividing both sides by N0:
110=e−λt2
- Taking the natural logarithm of both sides:
ln(110)=−λt2
- Therefore, we have:
t2=ln10λ
- Now we find the time necessary to decay from N02 to N010:
t2−t1=ln10λ−ln2λ
- Factoring out 1λ:
t2−t1=1λ(ln10−ln2)
- Using the property of logarithms lna−lnb=ln(ab):
t2−t1=1λln(102)=1λln5
- The half-life T is given by:
T=ln2λ⟹λ=ln2T
- Substituting λ into the equation for t2−t1:
t2−t1=Tln2ln5
Thus, the time necessary to decay from N02 atoms to N010 atoms is:
t2−t1=Tln5ln2
Topper's Solved these Questions
- BOOK - MTG-WBJEECHAPTER - NUCLEAR PHYSICEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS ( CATEGORY 1 : Single Option Correct Type )1videos
NUCLEAR PHYSIC
- BOOK - MTG-WBJEECHAPTER - MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTIONEXERCISE - WB-JEE Previous years questions17videos
MOTION OF CENTRE OF MASS, CONNECTED SYSTEMS, FRICTION
- BOOK - MTG-WBJEECHAPTER - OSCILLATIONS AND WAVESEXERCISE - WB JEE PREVIOUS YEARS QUESTIONS (CATEGORY 3: ONE OR MORE THAN ONE OPTION CORRECT TYPE (2 MARKS))2videos
OSCILLATIONS AND WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
The number of atoms of a radioactive substance at t = 0 is 8×104 . Its half- life periodis 4 years. The number of atoms left undecayed will be 1×104 after an interval of
A9 yearsB12 yearsC16 yearsDNone - Question 2 - Select One
The graph between number of decayed atoms N' of a radioactive element and time t is.
A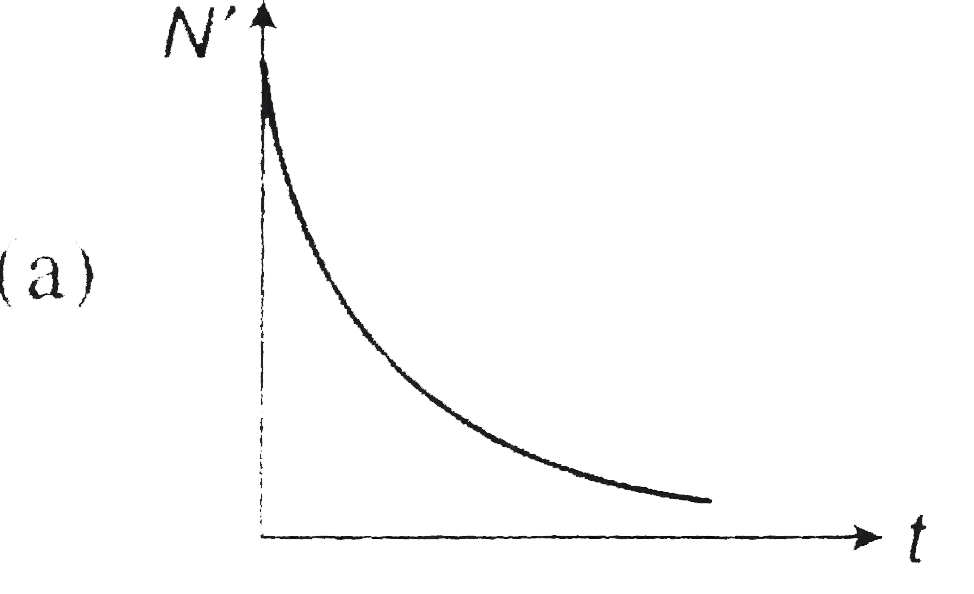 .B
.B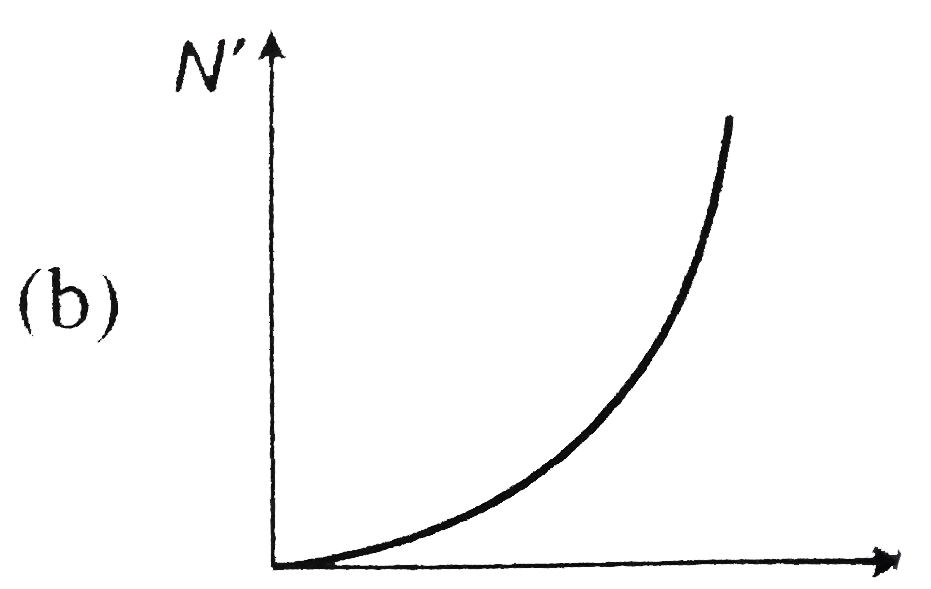 .C
.C .D
.D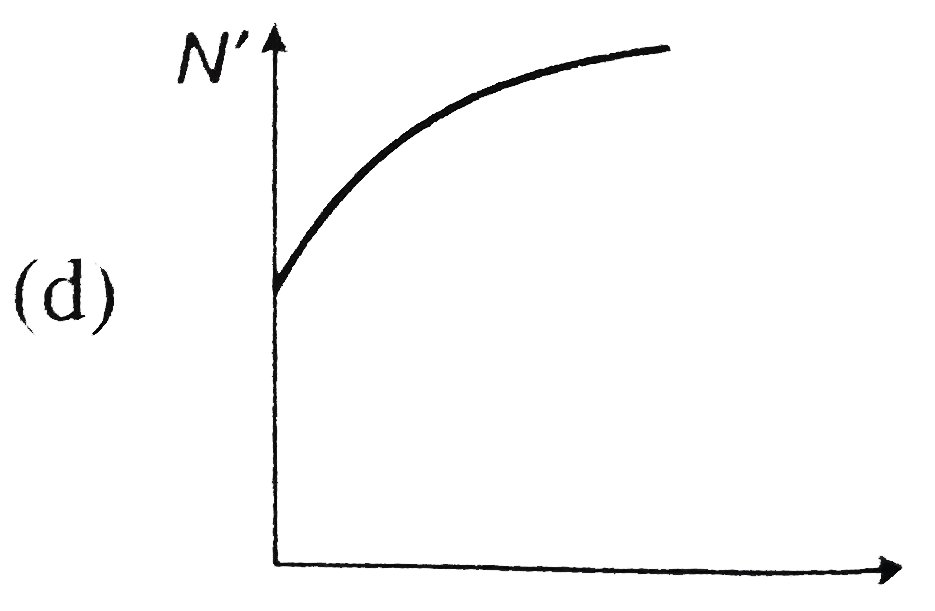 .
. - Question 3 - Select One
The half life of a radioactive substance is T0. At t=0,the number of active nuclei are N0. Select the correct alternative.
AThe number of nuclei decayed in time internal 0−t is N0e−λtBThe number of nuclei decays in time interval 0−t is N0(1−e−λt)CThe probability that a radioactive nuclei does not decay in interval 0−t is e−λtDThe probability that a radioactive nuclei does not decay in interval 1−e−λt
N atoms of a radioactive substance emit n α-particles per second. The half life of the radioactive substance is
View SolutionThe plot of the number (N) of decayed atoms versus activity (R) of a radioactive substance is
View SolutionThe number of atoms in 0.1 mol of a tetraatomic gas is (NA=6.02×1023mol−1)
View SolutionThe half life of radioactive substance is T. Then the fraction of the substance that has decayed in time t is-
View SolutionThe half-life of a sample of a radioactive substance is 1 hour. If 8×1010 atoms are present at t=0, then the number of atoms decayed in the duration t=2 hour to t=4 hour will be
View Solution

