The objective and eye piece of an astronomical telescope are double convexlenses with refractive jndex 1.5. When the telescope is adjusted to infinity the seperation between the lenses is 16 cm. If the space between the lenses is now filled with water and again telescope is adjusted for infinity. Then the present separation between the lenses is
8 cm
16 cm
24 cm
32 cm
The correct Answer is:D
To solve the problem, we need to determine the new separation between the objective and eyepiece lenses of an astronomical telescope after the space between them is filled with water. Here's the step-by-step solution:
Step 1: Understand the initial conditions
The initial separation between the lenses when adjusted for infinity is given as 16 cm. We denote this separation as S0=16cm.
Step 2: Refractive indices
The refractive index of the lenses (made of glass) is given as μ1=1.5. The refractive index of water is μ2=1.33. The refractive index of air is μ3=1.0.
Step 3: Use lens maker's formula
When the telescope is adjusted to infinity, the effective focal length F of the telescope can be expressed in terms of the focal lengths of the objective fo and the eyepiece fe:
1F=1fo+1fe
The total length of the telescope is given by:
S0=fo+fe
Step 4: Calculate the focal lengths
From the lens maker's formula, we know that the focal length f of a lens is given by:
f=R(μ−1)
where R is the radius of curvature of the lens and μ is the refractive index.
For the objective lens:
fo=Ro(1.5−1)=Ro0.5=2Ro
For the eyepiece lens:
fe=Re(1.5−1)=Re0.5=2Re
Step 5: Substitute into the total length equation
Substituting the focal lengths into the total length equation:
S0=fo+fe=2Ro+2Re=2(Ro+Re)
Since S0=16cm:
Ro+Re=8cm
Step 6: Adjust for water
When the space between the lenses is filled with water, we need to recalculate the effective focal lengths using the refractive index of water. The new focal lengths become:
f′o=Ro(1.33−1)=Ro0.33
f′e=Re(1.33−1)=Re0.33
Step 7: Calculate new total length
The new total length S′ of the telescope when filled with water is:
S′=f′o+f′e=Ro0.33+Re0.33=Ro+Re0.33
Substituting Ro+Re=8cm:
S′=80.33≈24.24cm
Step 8: Round to the nearest option
Since the options provided are 8 cm, 16 cm, 24 cm, and 32 cm, we round 24.24cm to the nearest option, which is 24 cm.
Final Answer
The present separation between the lenses when filled with water is 24 cm.
---
The initial separation between the lenses when adjusted for infinity is given as 16 cm. We denote this separation as S0=16cm.
The refractive index of the lenses (made of glass) is given as μ1=1.5. The refractive index of water is μ2=1.33. The refractive index of air is μ3=1.0.
When the telescope is adjusted to infinity, the effective focal length F of the telescope can be expressed in terms of the focal lengths of the objective fo and the eyepiece fe:
1F=1fo+1fe
The total length of the telescope is given by:
S0=fo+fe
From the lens maker's formula, we know that the focal length f of a lens is given by:
f=R(μ−1)
where R is the radius of curvature of the lens and μ is the refractive index.
fo=Ro(1.5−1)=Ro0.5=2Ro
fe=Re(1.5−1)=Re0.5=2Re
Substituting the focal lengths into the total length equation:
S0=fo+fe=2Ro+2Re=2(Ro+Re)
Since S0=16cm:
Ro+Re=8cm
When the space between the lenses is filled with water, we need to recalculate the effective focal lengths using the refractive index of water. The new focal lengths become:
f′o=Ro(1.33−1)=Ro0.33
f′e=Re(1.33−1)=Re0.33
The new total length S′ of the telescope when filled with water is:
S′=f′o+f′e=Ro0.33+Re0.33=Ro+Re0.33
Substituting Ro+Re=8cm:
S′=80.33≈24.24cm
Since the options provided are 8 cm, 16 cm, 24 cm, and 32 cm, we round 24.24cm to the nearest option, which is 24 cm.
The present separation between the lenses when filled with water is 24 cm.
Topper's Solved these Questions
- OPTICAL INSTRUMENTS BOOK - AAKASH SERIESCHAPTER - OPTICAL INSTRUMENTS EXERCISE - PRACTICE SHEET (EXERCISE -I) (OPTICAL INSTRUMENTS) (LEVEL-I (MAIN)) (SUBJECTIVE OBJECTIVE TYPE QUESTIONS)
21 Videos
- NUCLEIBOOK - AAKASH SERIESCHAPTER - NUCLEIEXERCISE - Practice Exercise
40 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - Exercise -I
10 Videos
Similar Questions
The focal lengths of the objective and the eyepiece of an astronomical telescope are 20 cm and 5 cm respectively. If the final image is formed at a distance of 30 cm from the eye piece, find the separation between the lenses for distinct vision:
View SolutionAn astronomical telescope is adjusted to form the final image at infinity. The separation between the lenses is 80 cm. The angular magnification is 15. Calculate the focal lengths of the objective lens and the eyepiece.
View SolutionThe focal length of objective and eye lens of a astronomical telescope are respectively 2m and 5cm . Final image is formed at (i) least distance of distinct vision (ii) infinity. The magnifying power in both cases will be
View SolutionThe focal length of objective and eye lens of a astronomical telescope are respectively 2m and 5cm . Final image is formed at (i) least distance of distinct vision (ii) infinity. The magnifying power in both cases will be
View SolutionAn astronomical telescope uses two lenses of powers 10 dioptre and I dioptre. If the final image of a distant object is formed at infinity, calculate the length of the telescope.
View Solution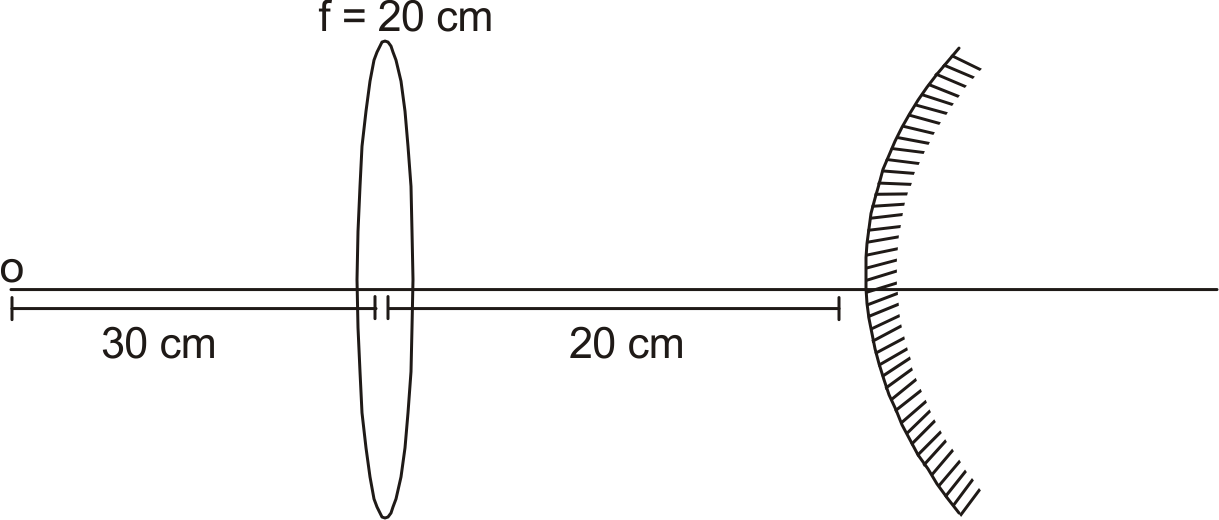
The lens shown is equiconvex having refractive Index. 1.5. In the situation shown the final image of object coincides with the object. The region between lens and mirror is now filled with a liquid of Rrefractive Index 2. Then find the separation between O & image formed by convex mirror.
View SolutionAn astronomical telescope consists of two thin convex lenses having focal lengths of 140 cm and 5 cm. The telescope is adjusted to be in normal adjustment.
What is the angular magnification, i.e.. magnifying power of the telescope in this set up?
(ii) What is the distance between the two lenses equal to ?
View SolutionThe magnifying power of an astronomical telescope is 8 and the distance between the two lenses is 54 cm. The focal length of eye lens and objective will be respectively.
View SolutionThe focal length of the objective and eye lenses of a microscope are 1.6 cm and 2.5 cm respectively. The distance between the two lenses is 21.7 cm. If the final image is formed at infinity. What is the linear magnification ?
View SolutionThe focal length of objective and the eyepiece of a compound microscope are 1cm and 5cm. An object is placed at a distance of 1.1 cm from the objective and if the final image is formed at infinity the magnifying power and distance between the lenses are respectively
View Solution
