The P−V diagram for a cyclic process is a triangle ABC drawn in order (figure). The co-ordinates of A,B,C are (4,1),(2,4)and(2,1) respectively. The co-ordinates are in the order (P,V) Pressure is in Nm−2 and volume is in liter. Calculate work done during the process from A to B, B to C and C to A. Also, calculate work done in the complete cycle.
To solve the problem step by step, we will calculate the work done during each segment of the cyclic process (A to B, B to C, and C to A) and then find the total work done in the complete cycle.
Step 1: Calculate Work Done from A to B
1. Identify Coordinates:
- A (4, 1)
- B (2, 4)
2. Determine the Area of Triangle ABC:
- The base of triangle AB is the difference in volume: VA−VB=4−2=2 liters.
- The height of triangle AB is the difference in pressure: PB−PA=4−1=3 Nm².
- Area of triangle AB = 12×base×height=12×2×3=3 Nm.
3. Convert Liters to Cubic Meters:
- Since 1 liter = 10−3 m³, we convert the area to Joules:
- Work done from A to B = 3×10−3 Joules.
Step 2: Calculate Work Done from B to C
1. Identify Coordinates:
- B (2, 4)
- C (2, 1)
2. Determine Work Done at Constant Pressure:
- The pressure during this process is constant at P=4 Nm².
- The volume change is VC−VB=1−4=−3 liters.
- Work done = P×ΔV=4×(−3)=−12 Nm.
3. Convert to Joules:
- Work done from B to C = −12×10−3 Joules.
Step 3: Calculate Work Done from C to A
1. Identify Coordinates:
- C (2, 1)
- A (4, 1)
2. Determine Work Done at Constant Volume:
- Since the volume does not change, the work done is 0 Joules.
Step 4: Calculate Total Work Done in the Complete Cycle
1. Sum the Work Done in Each Segment:
- Work done from A to B: 3×10−3 Joules
- Work done from B to C: −12×10−3 Joules
- Work done from C to A: 0 Joules
2. Total Work Done:
Wtotal=WAB+WBC+WCA=3×10−3−12×10−3+0=−9×10−3 Joules
Final Results
- Work done from A to B: 3×10−3 Joules
- Work done from B to C: −12×10−3 Joules
- Work done from C to A: 0 Joules
- Total work done in the complete cycle: −9×10−3 Joules
- A (4, 1)
- B (2, 4)
- The base of triangle AB is the difference in volume: VA−VB=4−2=2 liters.
- The height of triangle AB is the difference in pressure: PB−PA=4−1=3 Nm².
- Area of triangle AB = 12×base×height=12×2×3=3 Nm.
- Since 1 liter = 10−3 m³, we convert the area to Joules:
- Work done from A to B = 3×10−3 Joules.
- B (2, 4)
- C (2, 1)
- The pressure during this process is constant at P=4 Nm².
- The volume change is VC−VB=1−4=−3 liters.
- Work done = P×ΔV=4×(−3)=−12 Nm.
- Work done from B to C = −12×10−3 Joules.
- C (2, 1)
- A (4, 1)
- Since the volume does not change, the work done is 0 Joules.
- Work done from A to B: 3×10−3 Joules
- Work done from B to C: −12×10−3 Joules
- Work done from C to A: 0 Joules
Wtotal=WAB+WBC+WCA=3×10−3−12×10−3+0=−9×10−3 Joules
- Work done from B to C: −12×10−3 Joules
- Work done from C to A: 0 Joules
- Total work done in the complete cycle: −9×10−3 Joules
Topper's Solved these Questions
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Conceptual Problems
22 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Very short answer questions
31 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Curiosity Question
2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assertion- Reason Type questions
20 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assertion-Reason Type Questions
24 Videos
Similar Questions
Knowledge Check
An ideal gas is taken round a cyclic process represened by the triangle ABC drawn in order on a P-V diagram. The coordinates of A, B, C are (4,1), (2,4), (2,1) respectively. The work done in the complete cycle is
A9 unitsB6 unitsC3 unitsD0 unitsIf the co-ordinates of the vertices A,B,C of the triangle ABC are (−4,2),(12,−2)and(8,6) respectively, then∠B=
Atan−1(−67)Btan−1(67)Ctan−1(−76)Dtan−1(76)The co - ordinates of the centroid of a triangle ABC are (2,2) what are the co ordinates of vertex c if co ordinates of a and b (7,-1) and (1,2) respectively
A(−2,5)B(2,5)C(−2,−5)D(2,−5)
The area of triangle ABC is 25cm2 .The co-ordinates of vertex A are (-6,0) and B are (4,0). The vertex C lies on the line,x-y=4 .The co-ordinates of C are
View Solution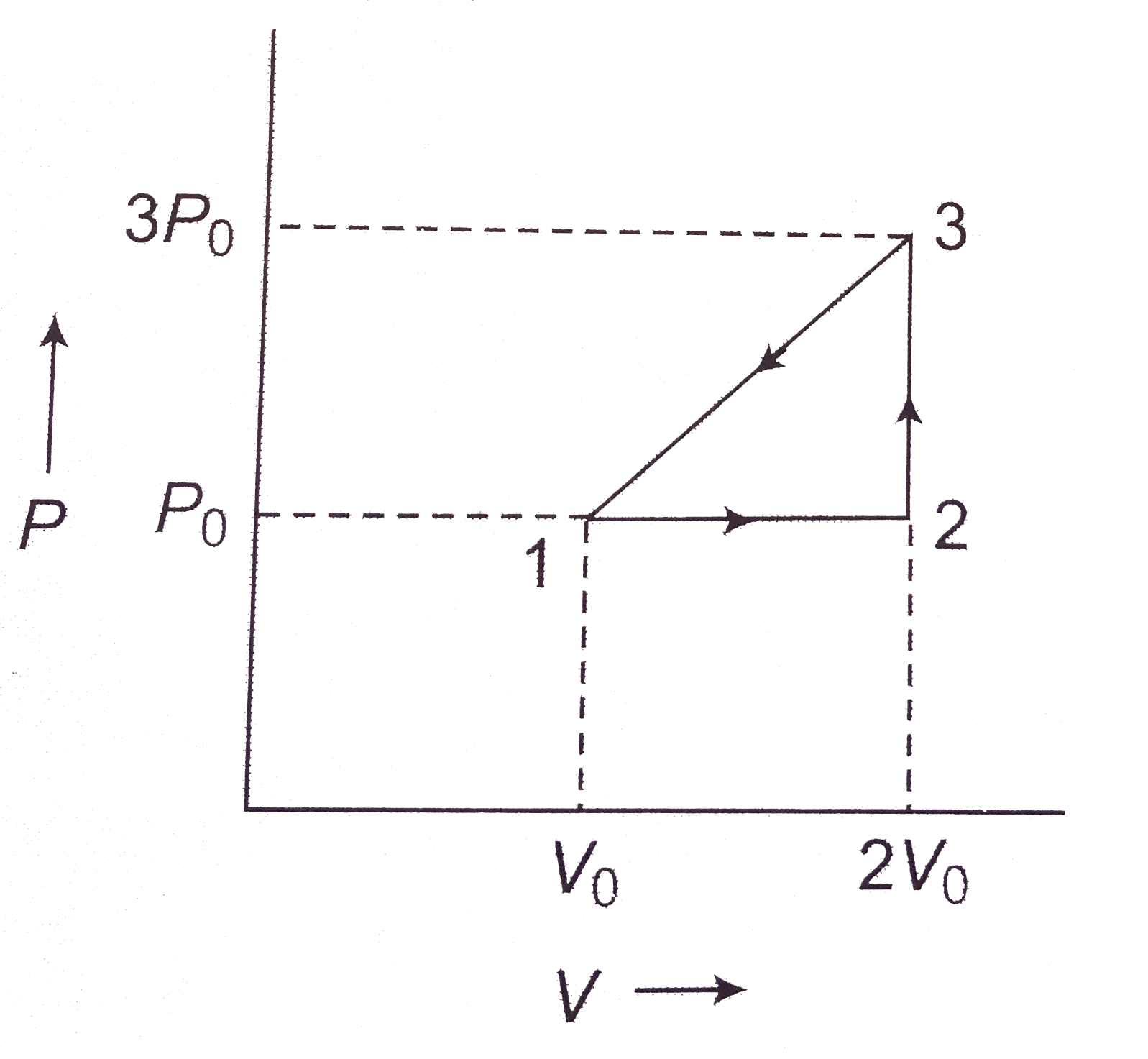
Calculate the work done by a gas as it is taken from 1 to 2,2 to 3 and 3 to 1 as shown. Also calculate the work done in cyclic process 1→2→3→1
View SolutionCalculate the work done in taking a charge of 0.02 C from A to B, if the potential at A is 20 V, and that at B is 30 V.
View SolutionThe co ordinates of the base BC of an isosceles triangle are B(1,3) and C(−2,7) then the co-ordinates of its vertex A are
View SolutionThe co- ordinates of the centroid of a triangle ABC are (2,2) . What are the co-ordinates of vertex C if co-ordinates of A and B are (7, - 1) and (1, 2) respectively ?
View Solution
