The path of a charged particle moving in a uniform steady magnetic field cannot be a
Let us visualise a uniform magnetic field within a given width as shown in the figure.
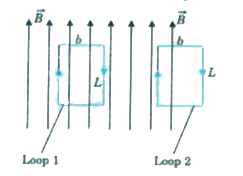
We have shown two Amperian loops in rectangular form with dimensions, L×b. Loop 1 is completely inside the magnetic field and loop 2 is at the boundary where magnetic field is shown to end abruptly.
First of all let us look at loop 1. Two sides of this loop are perpendicular to the magnetic field and hence →B⋅d→l=0 for these two sides. Let the sense of the loop assumed be as shown in the figure so →B⋅d→l for the remaining one arm is BL and for the other it is−BL and these two add up to zero. Hence total circulation of magnetic field is zero for loop A.
According to Ampere.s law, the circulation of magnetic field must be equal to Ho multiplied with enclosed current. Hence, the enclosed current in loop A must be zero. From this condition we can conclude that there will not be any current inside the uniform magnetic field.
Now let us look at loop 2. One side of loop 2 is outside the field and similar to loop A, if we calculate then we will get the net circulation for loop B equal to BL, because one side is outside the field and there is no cancellation like in loop 1. It is non-zero. Again, according to Ampere.s law there must be some enclosed current within this Amperian loop B due to non-zero circulation of magnetic field. But we have already proved that no current will be enclosed within the uniform field. Hence, there is discrepancy near the boundary. The fact is that a uniform magnetic field can never end abruptly like this in real life.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT FILE (NCERT Textbook Exercises)13videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT FILE (NCERT Additional Exercises)15videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Conceptual Questions29videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
Similar Questions
What is the path of a charged particle moving in a uniform magnetic field with initial velocity (i) parallel to the field? (ii) perpendicular to the field? (iii) at some angle with the direction of magnetic field.
View SolutionDescribe the path of a charged particle moving in a uniform magnetic field with initial velocity
(i) parallel to (or along) the field.
(ii) perpendicular to the field.
(iii) at an arbitrary angle θ(0∘<θ<90∘).View Solution
Knowledge Check
- Question 1 - Select One
Statement-1 Path of a charged particle in a uniform and steady magnetic field cannot be parabolic
Statement-2 Magnetic field cannot accelerate a charged particleAStatement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1BStatement-1 is True, Statement-2, is True, Statement-2 is NOT a correct explanation for Statement-1CStatement-1 is True, Statement-2 is FalseDStatement-1 is False, Statement-2 is True - Question 2 - Select One or More
The radius of curvature of the path of a charged particle moving in a static uniform magnetic field is
ADirectly proportional to the magnitude of the charge on the particleBDirectly proportional to the magnitude of the linear momentum of the particleCDirectly proportional to the kinetic energy of the particleDInversely proportional to the magnitude of the magnetic field - Question 3 - Select One or More
The radius of curvature of the path of a charged particle moving in a static uniform magnetic field is
ADirectly propotional to the magnitude of the charge on the particleBDirectly propotional to the magnitude of the liner momentum of the particleCDirectly proportional to the kinetic energy of the particleDInversely proportional to the magnitude of the magnetic field
What will be the path of a charged particle moving perpendicular to a uniform magnetic field?
View SolutionThe radius of curvature of the path of a charged particle moving under a uniform , normal magnetic field is directly proportional to
View SolutionA particle is moving in a uniform magnetic field, then
View SolutionAssertion: The energy of charged particle moving in uniform magnetic field does not change.
Reason: Work done by magnetic field on the charge is zero.View SolutionAssertion : Path of a charged particle in uniform magnetic field cannot be a parabola.
Reason : For parabolic path acceleration should be constant.View Solution

