The perpendicular distance between the incident ray and the emergent ray in a glass slab is called the ..................... (angle of emergence/lateral displacement).
To solve the question, we need to identify the term that describes the perpendicular distance between the incident ray and the emergent ray in a glass slab. Let's break it down step by step:
Step 1: Understand the Terms
- Incident Ray: This is the ray of light that strikes the surface of the glass slab.
- Emergent Ray: This is the ray of light that exits the glass slab after refraction.
Step 2: Visualize the Situation
- Imagine a glass slab where a ray of light enters (incident ray) and then exits (emergent ray) after bending due to refraction at the boundaries of the slab.
Step 3: Define the Perpendicular Distance
- The question specifically asks for the perpendicular distance between the path of the incident ray (if extended) and the path of the emergent ray.
Step 4: Identify the Correct Term
- The term that describes this perpendicular distance is known as lateral displacement. It refers to the horizontal shift of the light ray as it passes through the slab.
Final Answer
The perpendicular distance between the incident ray and the emergent ray in a glass slab is called the lateral displacement.
---
- Incident Ray: This is the ray of light that strikes the surface of the glass slab.
- Emergent Ray: This is the ray of light that exits the glass slab after refraction.
- Imagine a glass slab where a ray of light enters (incident ray) and then exits (emergent ray) after bending due to refraction at the boundaries of the slab.
- The question specifically asks for the perpendicular distance between the path of the incident ray (if extended) and the path of the emergent ray.
- The term that describes this perpendicular distance is known as lateral displacement. It refers to the horizontal shift of the light ray as it passes through the slab.
The perpendicular distance between the incident ray and the emergent ray in a glass slab is called the lateral displacement.
Similar Questions
The angle between the incident ray and the emergent ray in case of a prism is called angle of prism. _________
View SolutionThe angle between the incident ray and the refracted ray of a prism is called angle of deviation.
View SolutionThe angle between the incident ray and emergent ray, when the ray is passing through an equilateral prism is called angle of _____.
View Solution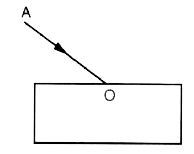
In the adjacent diagram, AO is a ray of light incident on a rectangular glass slab.
(a) Complete the path of the ray till it emerges out of the slab.
(b) In the diagram, mark the angle of incidence (i) and the angle of refraction (r) at the first interface. how is the refractive index of glass related to the angles i and r ?
(c) Mark angle of emergence by the letter e. how are the angles i and e related ?
(d) Which two rays are parallel to each other ? Name them
(e) Indicate in the diagram the lateral displacement between the emergent ray and the incident ray. state one factor that affects the lateral displacement.
View SolutionThe refracting angle of a glass prism is 30∘. A ray is incident onto one of the faces perpendicular to it. Find the angle δ between the incident ray and the ray that leaves the prism. The refractive index of glass is μ=1.5.
View SolutionThe refracting angle of a glass prism is 30∘. A ray is incident onto one of the faces perpendicular to it. Find the angle δ between the incident ray and the ray that leaves the prism. The refractive index of glass is μ=1.5.
View SolutionDraw a diagram to show refraction through a glass slab and label the following: (a) incident ray (b) refracted ray (c) emergent ray (d) angle of incidence (e) angle of refraction at the first boundary of two mediums (f) angle of emergence and (g) lateral displacement
View SolutionA ray of light strikes a glass slab 5 cm thick, making an angle of incidence equal to 30∘.
(a) Draw a ray diagram showing the emergent ray and the refracted ray through the glass block. The refractive index of glass is 1⋅5.
(b) Measure the lateral displacement of the ray. The sin 19⋅5∘=1/3.
View SolutionA ray of light is incident at an angle of 60∘ on the face of a prism having refracting angle 30∘. The ray emerging out of the prism makes an angle 30∘ with the incident ray. Show that the emergent ray is perpendicular to the face through which it emerges and calculate the refractive index of the material of prism.
View SolutionA ray of light is incident at an angle of 60∘ on the face of a prism having refracting angle 30∘. The ray emerging out of the prism makes an angle 30∘ with the incident ray. Show that the emergent ray is perpendicular to the face through which it emerges and calculate the refractive index of the material of prism.
View Solution
