The phase difference between two particle executing SHM of the same amplitude and frequency along same straight line while pessing one another when going in apposition direction with equal displacement from then respectively straing about is is 2π/3 if the prass if one particle is π/6 find the displecement at this instant amplitude is A
A/3
2A/3
3A/4
A/2
The correct Answer is:D
Phase difference δ=2π3=δ2−δ1=δ2
=δ2−π6⇒δ2−5π6,sinδ1=sinδ2=12
Displacement is measured from starting, point (t=0)
So, s=Asin(ωt+δ1),Asin(0+π6)=A2
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Velocity , Acceleration And Energy Of Simple Harmonic Motion40videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Spring Particle System24videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
Similar Questions
Two particles execute SHMs of the same amplitude and frequency along the same straight ling. They cross one another when going in opposite direction. What is th ephase difference between them when their displacements are half of their amplitudes ?
View SolutionTwo particles execute SHM of same amplitude and frequency on parallel lines. They pass one another when moving in opposite directions each time their displacement is one thhird their amplitude. What is the phase difference between them?
View Solution
Knowledge Check
- Question 1 - Select One
Two particles executes S.H.M. of the same amplitude and frequency along the same straight line. They pass one another when going in opposite directions, each time their displacement is root three by two times amplitude. The phase difference between them is
A2π3 radBπ2 radCπ6 radDπ3 rad - Question 2 - Select One
Two particles execute SHM of the same time period along the same straight lines. They cross each other at the mean position while going in opposite directions. Their phase difference is
Aπ2BπC3π2D2π - Question 3 - Select One
Two particles execute simple harmonic motion of the same amplitude and frequency along close parallel lines. They pass each other moving in opposite directions each time their displacement is half their amplitude. Their phase difference is
A5π6B4π3Cπ6D2π3
Find the phase different between two particles executing simple harmonic motion with the same amplitude and frequency when their phases at a certain moment are as shown in the figure.
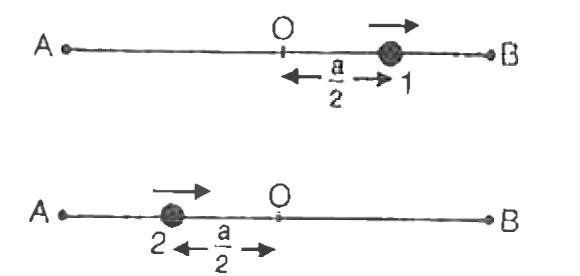 View Solution
View Solutiontwo particle executing SHM with same frequency and amplitudes Aand2A on same straight line with same mean position cross each other in opposite direction at a distance A/3 from mean position. Find the phase difference in the two SHM s.
View SolutionTwo particles P and Q describe S.H.M. of same amplitude a, same frequency f along the same straight line from the same mean position. The maximum distance between the two particles is a √2, If the initial phase difference between the particles is πN then find N :
View SolutionTwo particles execute S.H.M. along the same line at the same frequency. They move in opposite direction at the mean position. The phase difference will be :
View SolutionTwo particles P and Q describe SHM of same amplitude a frequency ν along the same straight line. The maximum distance between two particles is √2a. The initial phase difference between the particles is
View Solution

