The plates of a parallel plate capacitor with air as medium are separated by a distance of 8mm. A medium of dielectric constant 2 and thickness 4mm having the same area is introduced between the plates. For the capacitance to remain the same, the distance between the plates is
8 mm
6 mm
4 mm
10 mm
The correct Answer is:D
Original capacity, with air
C=ε0Ad
When dielectric plate (medium) of thickness t is introduced between the plates, then capacity becomes
C'=ε0Ad'−t(1−1K)
But as given, C'=C
∴ε0Ad=ε0Ad'−t(1−1K)
ord=d'−1+42⇒8=d'−2ord'=10 mm
Topper's Solved these Questions
Similar Questions
The two plates of a parallel plate capacitor are 4mm apart. A slab of dielectric constant 3 and thickness 3mm is introduced between the plates is so adujected that the capacitance of the capacitor becomes 23rd of its original value. What is the new distance between the plates ?
View SolutionThe two plates of a parallel plate capacitor are 4 mm apart . A slab of dielectric constant 3 and thickness 3 mm is introduced between the plates with its face parallel to them . The distance between the plates is so adjusted that the capacity of the capacitor becomes 23 rd of its original value . What is the new distance the plates ?
View Solution
Knowledge Check
Separation between the plates of a parallel plate capacitor is d and the area of each plates is A. When a slab of material of dielectric constant k and thickness t(t<d) is introduced between the plates. Its capacitance becomes
Aε0Ad+t(1−1k)Bε0Ad+t(1+1k)Cε0Ad−t(1−1k)Dε0Ad−t(1+1k)The capacitance of a parallel plate condenser with a separation of 4 mm between the plates is 7μF. If a mica sheet (K=6) of thickness 2 mm and of the same area is introduced betwenn the plates, its capacitance will be
A6μFB9μFC12μFD15μFThe separation between the plates of a parallel plate capacitor is d and the area of each plate is A. iff a dielectric slab of thickness x and dielectric constant K is introduced between the plates, then the capacitance will be
Aε0Ad−x(1−1K)Bε0Ad+x(1−1K)Cε0Ad+x(1+1K)Dε0Ad−x(1+2K)
Two metal plates form a parallel plate capacitor. The distance between the plates is d. A metal sheet of thickness d/2 and of the same area is indroduced between the plates. What is the ratio of the capacitances in the two cases?
View SolutionA parallel plate capacitor with air as the dielectric has capacitance C. A slab of dielectric constant K and having the same thickness as the separation between plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. The new capacitance will be :
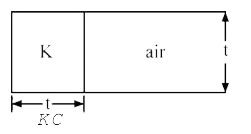
View SolutionA parallel plate capacitor has a capacitance of 60 PF, when the plates of the capacitor and separated by a distance d. if a metal plate of thickness t=d3 is introduced between the plates, the capacitance will be
View SolutionA parallel plate capacitor with vacuum between its plates has capacitance C. A slabe of dielectric constant K and having the same thickness as the separation between the plates is introduced so as to fill 1/3rd of the capacitor as shown in the figure. the new capacitance will be
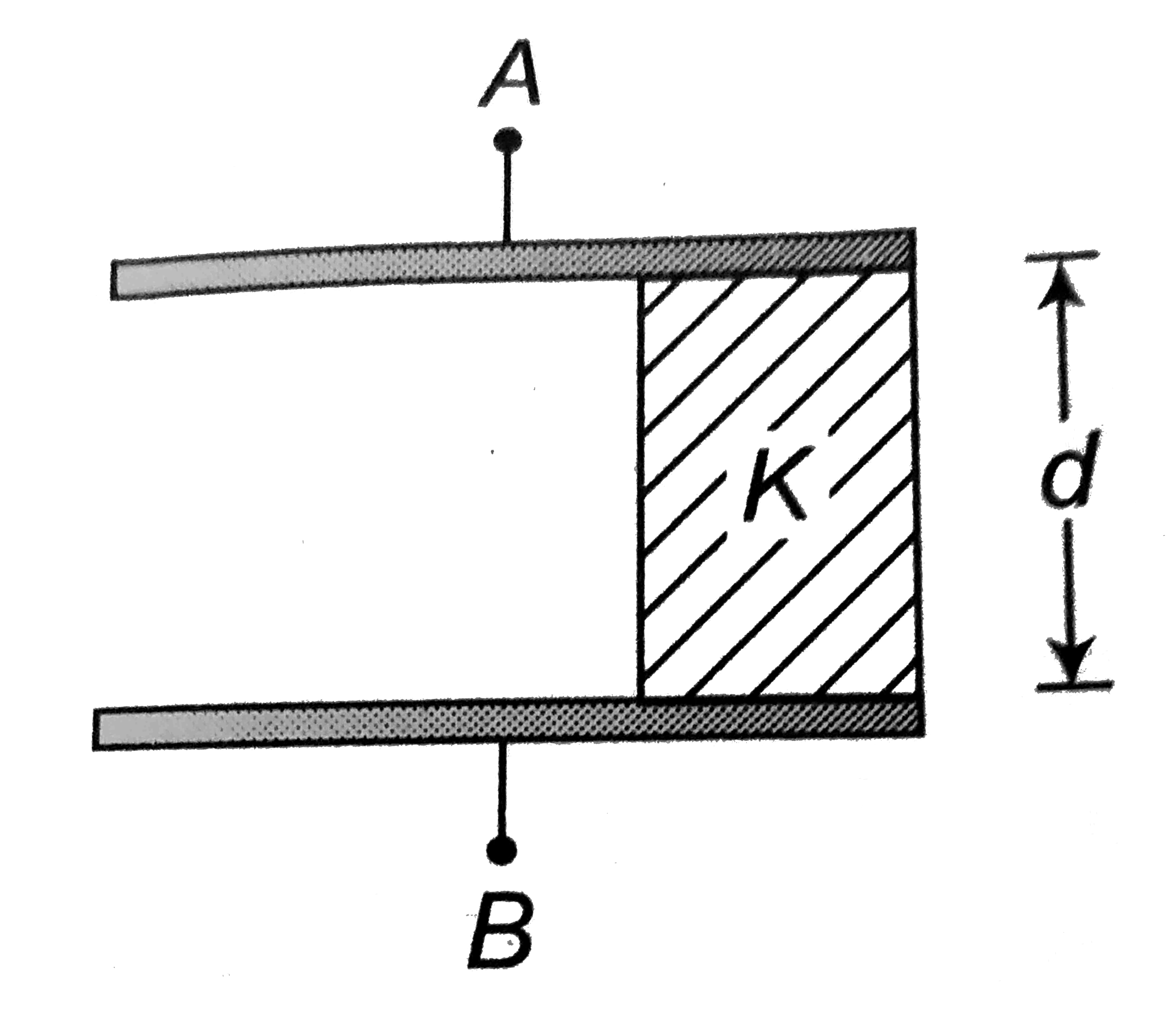
View SolutionTwo metal plates are separated by a distance d in a parallel plate condenser. A metal plate of thickness t and of the same area is inserted between the condenser plates. The value of capacitance increases by ….times.
View Solution
