The position-time relation of a particle moving along the x-axis is given by
x=a−bt+ct2
where a, b and c are positive numbers. The velocity-time graph of the particle is
A
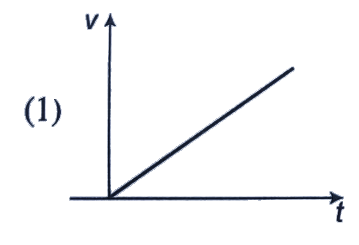
B
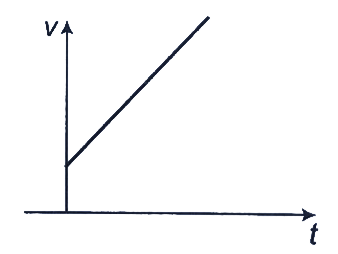
C
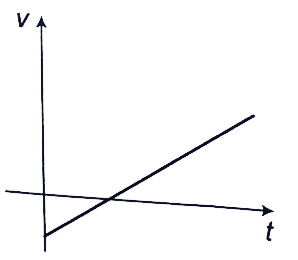
D
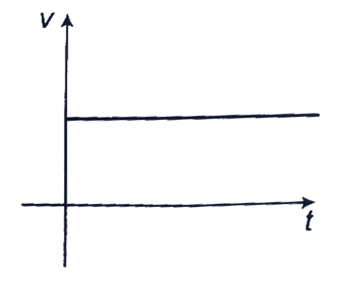
Video Solution
Text Solution
The correct Answer is:C
x=a−bt+ct2
v=dxdt=−b+2ct
v-t graph
y=−b+2cx, straight line
y=C+mx
Slope m=2c, +ve
Intercept, c=−b, -ve
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The displacement of a particle moving along x-axis is given by :
x=a+bt+ct2
The acceleration of the particle is.AbBcCb+cD2 c - Question 2 - Select One
The displacement x of a particle at time t moving along a straight line path is given by x2=at2+2bt+c where a, b and c are constants. The acceleration of the particle varies as
Ax−1Bx−2Cx−3Dx−4 - Question 3 - Select One
The position x of particle moving along x-axis varies with time t as x=Asin(ωt) where A and ω are positive constants. The acceleration a of particle varies with its position (x) as
Aa=AxBa=−ω2xCa=AωxDa=ω2xA
The position of a particle moving along the y-axis is given as y=3t2−t3 where y is in , metres and t is in sec.The time when the particle attains maximum positive y position will be
View SolutionThe position of a particle moving along x-axis is given by x=10t−2t2. Then the time (t) at which it will momentily come to rest is
View SolutionFigure shows the position of a particle moving on the x - axis as a function of time
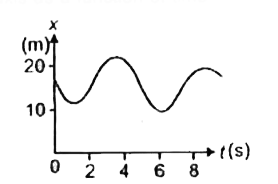 View Solution
View SolutionThe reation between the time t and position x for a particle moving on x-axis is given by t=px2+qx, where p and q are constants. The relation between velocity v and acceleration a is as
View SolutionFigure shows the position of a particle moving on the X-axis as a function of time.
 View Solution
View Solution

