The position vector of a particle at two points along its path is given along with the time taken to move from one point to other . Can we determine particle's instantaneous velocity and its average velocity using this data? Explain.
To determine the average and instantaneous velocity of a particle given its position vectors at two points and the time taken to move between them, we can follow these steps:
1. Identify the Position Vectors:
Let the position vector of the particle at point 1 be denoted as O1 and at point 2 as O2.
2. Calculate the Displacement:
Displacement d is defined as the difference between the final and initial position vectors:
d=O2−O1
3. Determine the Time Interval:
Let t be the time taken to move from point 1 to point 2. This value is given in the problem.
4. Calculate the Average Velocity:
Average velocity vavg can be calculated using the formula:
vavg=DisplacementTime=dt=O2−O1t
This gives us the average velocity vector.
5. Understanding Instantaneous Velocity:
Instantaneous velocity is defined as the velocity of the particle at a specific instant. To determine instantaneous velocity, we need to know the exact path taken by the particle between the two points. Since we only have the initial and final position vectors and the time taken, we cannot determine the instantaneous velocity without additional information about the path.
6. Conclusion:
We can determine the average velocity using the given data, but we cannot determine the instantaneous velocity due to the lack of information about the path taken by the particle.
Let the position vector of the particle at point 1 be denoted as O1 and at point 2 as O2.
Displacement d is defined as the difference between the final and initial position vectors:
d=O2−O1
Let t be the time taken to move from point 1 to point 2. This value is given in the problem.
Average velocity vavg can be calculated using the formula:
vavg=DisplacementTime=dt=O2−O1t
This gives us the average velocity vector.
Instantaneous velocity is defined as the velocity of the particle at a specific instant. To determine instantaneous velocity, we need to know the exact path taken by the particle between the two points. Since we only have the initial and final position vectors and the time taken, we cannot determine the instantaneous velocity without additional information about the path.
We can determine the average velocity using the given data, but we cannot determine the instantaneous velocity due to the lack of information about the path taken by the particle.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - TOUGH & TRICKY PROBLEMS14videos
MOTION IN A PLANE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - NCERT FILE (Solved) NCERT (Textbook Exercises)25videos
MOTION IN A PLANE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - PRACTICE PROBLEMS2videos
MOTION IN A PLANE
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test16videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST16videos
MOTION IN A STRAIGHT LINE
Similar Questions
The position-time graph of a moving particle is a shown. The instantaneous velocity of the particle is negative at the point.
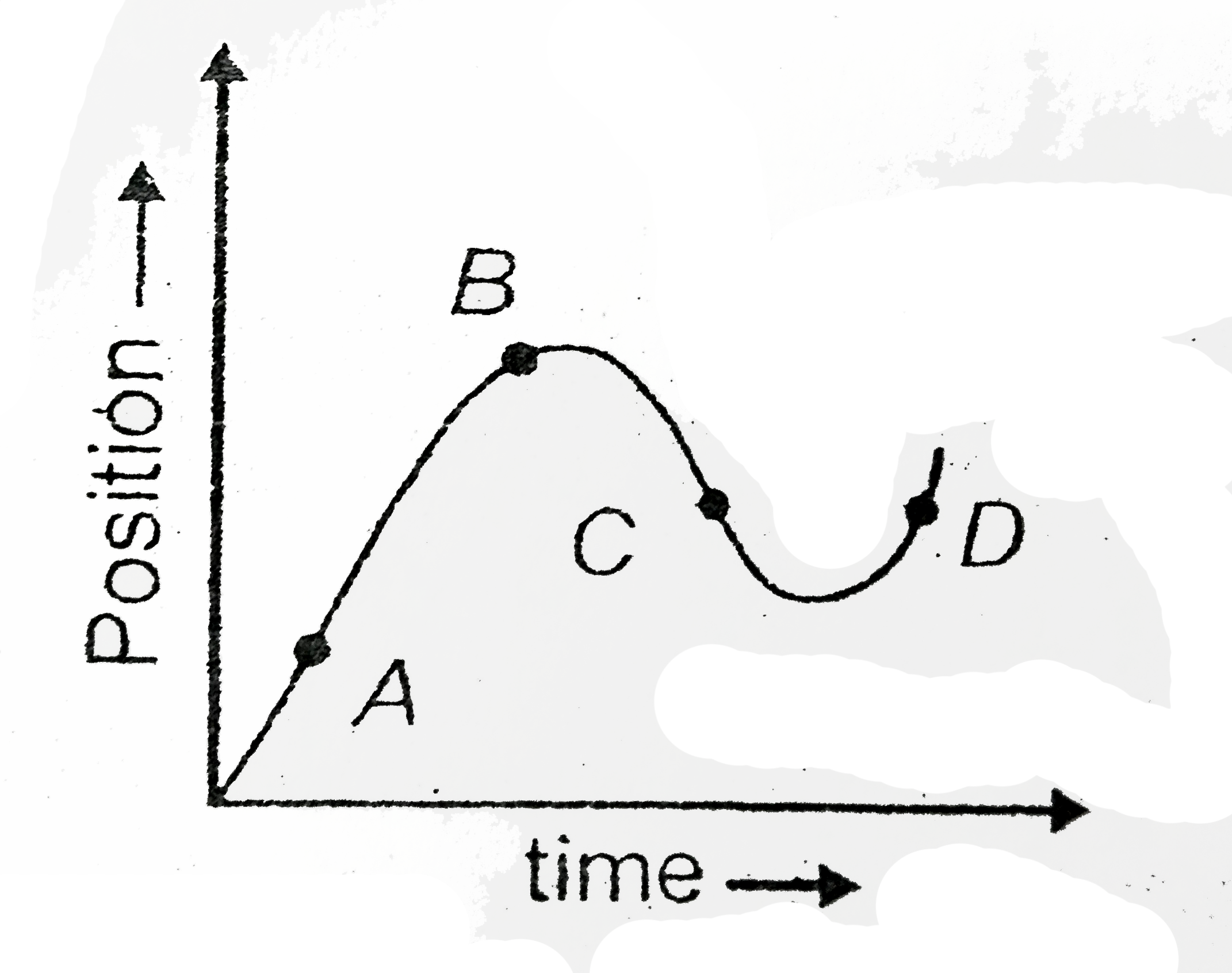 View Solution
View SolutionWhen a particle moves with constant velocity, its average velocity, its instantaneous velocityi and its speed are all equal. Comment on this statement.
View Solution
Knowledge Check
- Question 1 - Select One
The position- time graph of a moving particle is shown. The instantaneous velocity of the particle is negative at the point
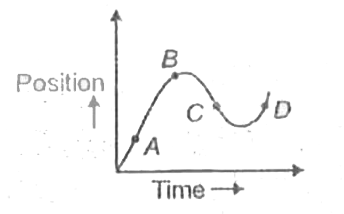 AABBCCDD
AABBCCDD - Question 2 - Select One
If a particle is moving along a circular path with constant speed, then Its motion is
APeriodic and simple harmonicBNon periodicCPeriodic but not simple harmonicDNon periodic but simple harmonic - Question 3 - Select One
The trajectory of a particle moving in vast maidan is as shown in the figure. The coordinates of a position A are (0,2). The coordinates of another point at which the instantaneous velocity is same as the average velocity between the points are
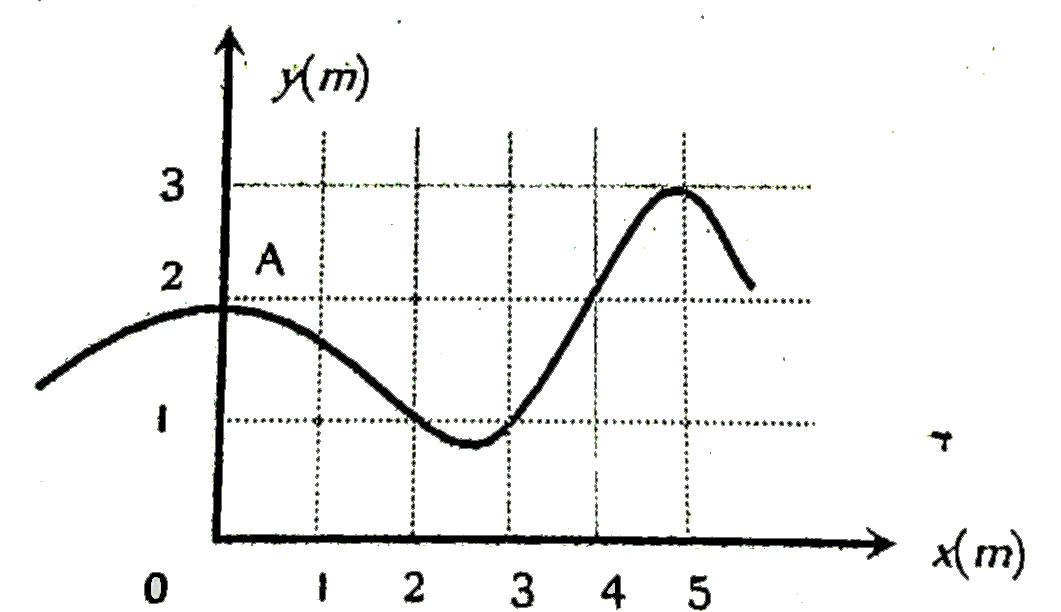 A(1,4)B(5,3)C(3, 4)D(4, 1)
A(1,4)B(5,3)C(3, 4)D(4, 1)
When a particle moves with constant velocity its average velocity, its instantaneous velocity and its speed all are equal. Is this statement true or false ?
View SolutionAssertion: The instantaneous velocity does not depend on instantaneous position vector.
Reason: The instantaneous velocity and average velocity of a particle are always same.View SolutionThe velocity-time graph of a particle moving along a straight line is given as below. The displacement time curve for the particle is given by :
 View Solution
View SolutionA man moves in x−y plane along the path shown. At what points is his average velocity vector in the sam direction as his instantaneous velocity vector. The man starts from point P.
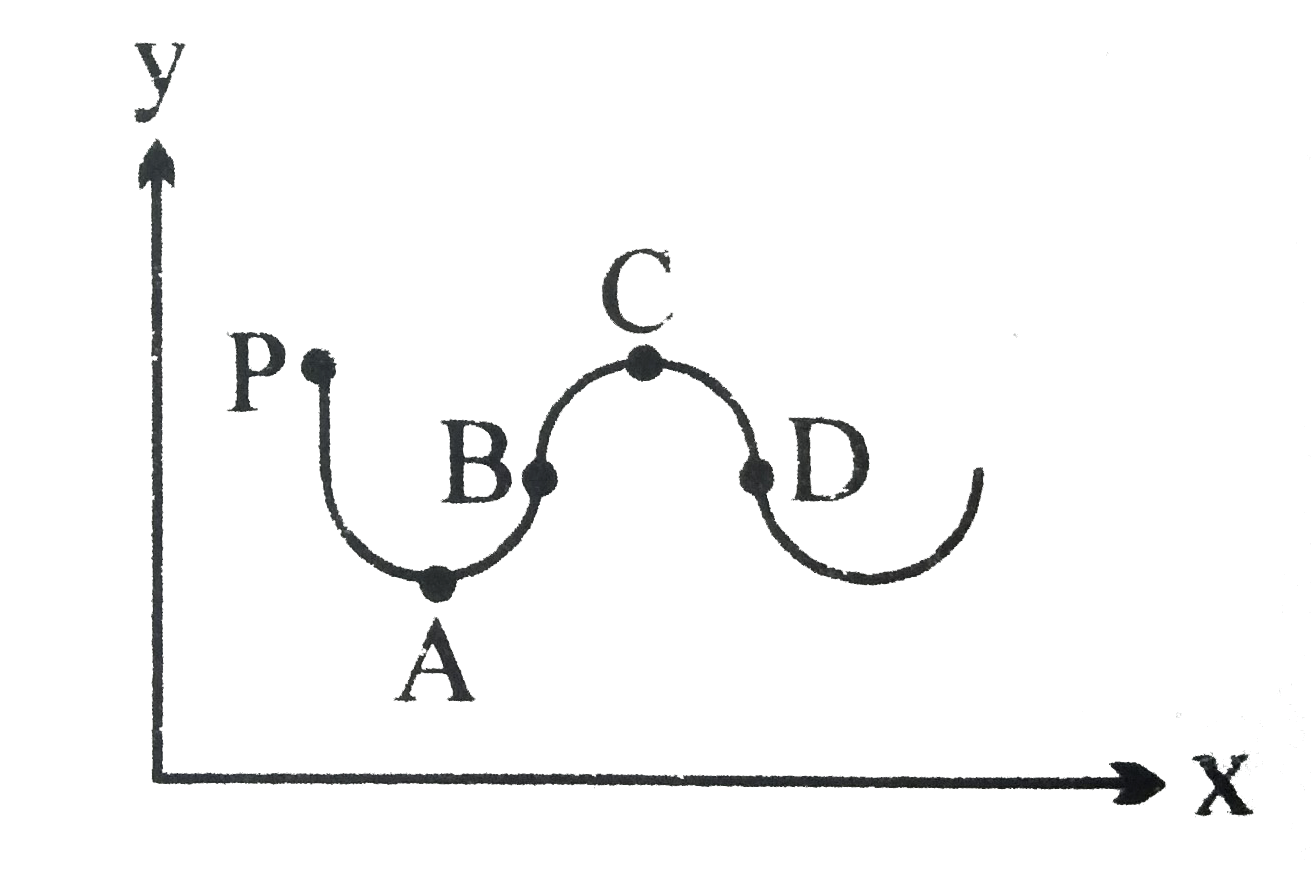 View Solution
View SolutionA particle moves on a path as shown. The particle takes 10 seconds in going from starting point to the final point. What is the average velocity vector of the particle ?
 View Solution
View Solution

