The position vector $\to r = 5.00 t ˆ i + (e t + f t^{2}) ˆ j$ locates a particle as a function of time t. Vector $\to r$ is in meters, t is in seconds, and factors e and f are constants. Figure 4-27 gives the angle $θ$ of the particle's direction of travel as a function of t ( $θ$ is measured from the positive x direction). What are (a) e and (b) f, including units?

Video Solution

Text Solution

Verified by Experts

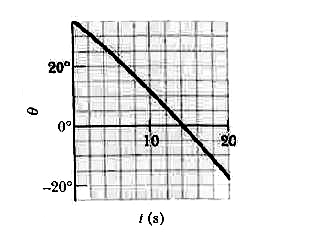
(a) 3.50 m/s, (b) $- 0.125 m / s^{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS MOTION IN TWO AND THREE DIMENSIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
Position vector of a particle is expressed as function of time by equation $\to r = 2 t^{2} + (3 t - 1) ˆ j + 5 ˆ k$ . Where r is in meters and t is in seconds.
AIt always moves in a plane that is parallel to the x-y plane.
BAt the instant t=0 s, it is observed at point (0m, -1m, 5m), moving with velocity 3 m/s in the positive y-direction.
CIts acceleration vector is uniform.
DIt is an example of three dimensional motion.
Question 2 - Select One
A particle moves in a plane such that its coordinates changes with time as $x = a t$ and $y = b t$ , where a and b are constants. Find the position vector of the particle and its direction at any time t.
A $(a) ˆ i + (b t) ˆ j$
B $(a t) ˆ i + (b) ˆ j$
C $(a t) ˆ i + (b t) ˆ j$
D $(a) ˆ i + (b) ˆ j$
Question 3 - Select One
The position vector of a particle is given by $\to r = {\to r}_{0}$ (1-at)t, where t is the time and a as well as ${\to r}_{0}$ are constant. After what time the particle retursn to the starting point?
Aa
B $\frac{1}{a}$
C $a^{2}$
D $\frac{1}{a^{2}}$

RESNICK AND HALLIDAY-MOTION IN TWO AND THREE DIMENSIONS-PROBLEMS

Home
Ask Doubt
Profile