The potential difference across the terminals of a battery of emf12V and internal resistance 2Ω drops to 10V when it is connected to a silver voltameter. Find the silver deposited at the cathode in half an hour. Atomic weight of silver is 107.9gmol−1.
The correct Answer is:B
To solve the problem step by step, we will follow these calculations:
Step 1: Determine the Current Flowing Through the Circuit
We start with the formula for the electromotive force (emf) of the battery:
E=I⋅r+V
Where:
- E = emf of the battery = 12 V
- r = internal resistance = 2 Ω
- V = potential difference across the terminals = 10 V
- I = current (unknown)
Rearranging the equation to find the current I:
I=E−Vr
Substituting the known values:
I=12V−10V2Ω=2V2Ω=1A
Step 2: Calculate the Electrochemical Equivalent of Silver
The mass of silver deposited can be calculated using Faraday's laws of electrolysis:
M=Z⋅I⋅T
Where:
- M = mass of silver deposited
- Z = electrochemical equivalent
- I = current = 1 A (from Step 1)
- T = time in seconds = 30 minutes = 1800 seconds
To find Z, we use the formula:
Z=EF
Where:
- E = equivalent weight of silver = 107.9 g/mol1=107.9 g/mol (since the valency of silver is 1)
- F = Faraday's constant = 96500 C/mol
Calculating Z:
Z=107.9 g/mol96500 C/mol≈0.00112 g/C
Step 3: Substitute Values to Find the Mass of Silver Deposited
Now we can substitute the values into the equation for mass M:
M=Z⋅I⋅T
Substituting the known values:
M=0.00112 g/C⋅1 A⋅1800 s
Calculating M:
M=0.00112⋅1800≈2.016 g
Final Answer
The mass of silver deposited at the cathode in half an hour is approximately 2 grams.
---
We start with the formula for the electromotive force (emf) of the battery:
- E = emf of the battery = 12 V
- r = internal resistance = 2 Ω
- V = potential difference across the terminals = 10 V
- I = current (unknown)
The mass of silver deposited can be calculated using Faraday's laws of electrolysis:
- M = mass of silver deposited
- Z = electrochemical equivalent
- I = current = 1 A (from Step 1)
- T = time in seconds = 30 minutes = 1800 seconds
- E = equivalent weight of silver = 107.9 g/mol1=107.9 g/mol (since the valency of silver is 1)
- F = Faraday's constant = 96500 C/mol
Now we can substitute the values into the equation for mass M:
The mass of silver deposited at the cathode in half an hour is approximately 2 grams.
Topper's Solved these Questions
- THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTBOOK - HC VERMA ENGLISHCHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Short Question
9 Videos
- THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTBOOK - HC VERMA ENGLISHCHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Objective 2
5 Videos
- THE SPECIAL THEORY OF RELATIVITYBOOK - HC VERMA ENGLISHCHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Short answer
2 Videos
- X-RaysBOOK - HC VERMA ENGLISHCHAPTER - X-RaysEXERCISE - Ques for Short Ans
10 Videos
Similar Questions
The potential difference between the terminals of a battery of emf 6.0V and internal resistance1(Ω)drops to 5.8 V when connected across an external resistor. Find the resistance of the external resistor.
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionA battery of emf 2.0V and internal resistance 0.10Ω is being charged with a current of 5.0A. Find the potential difference between the terminals of the battery?
View SolutionA car battery of emf 12V and internal resistance 0.05ω receives a current of 60 A from an external source, then the terminal potential difference of the battery is
View SolutionA battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
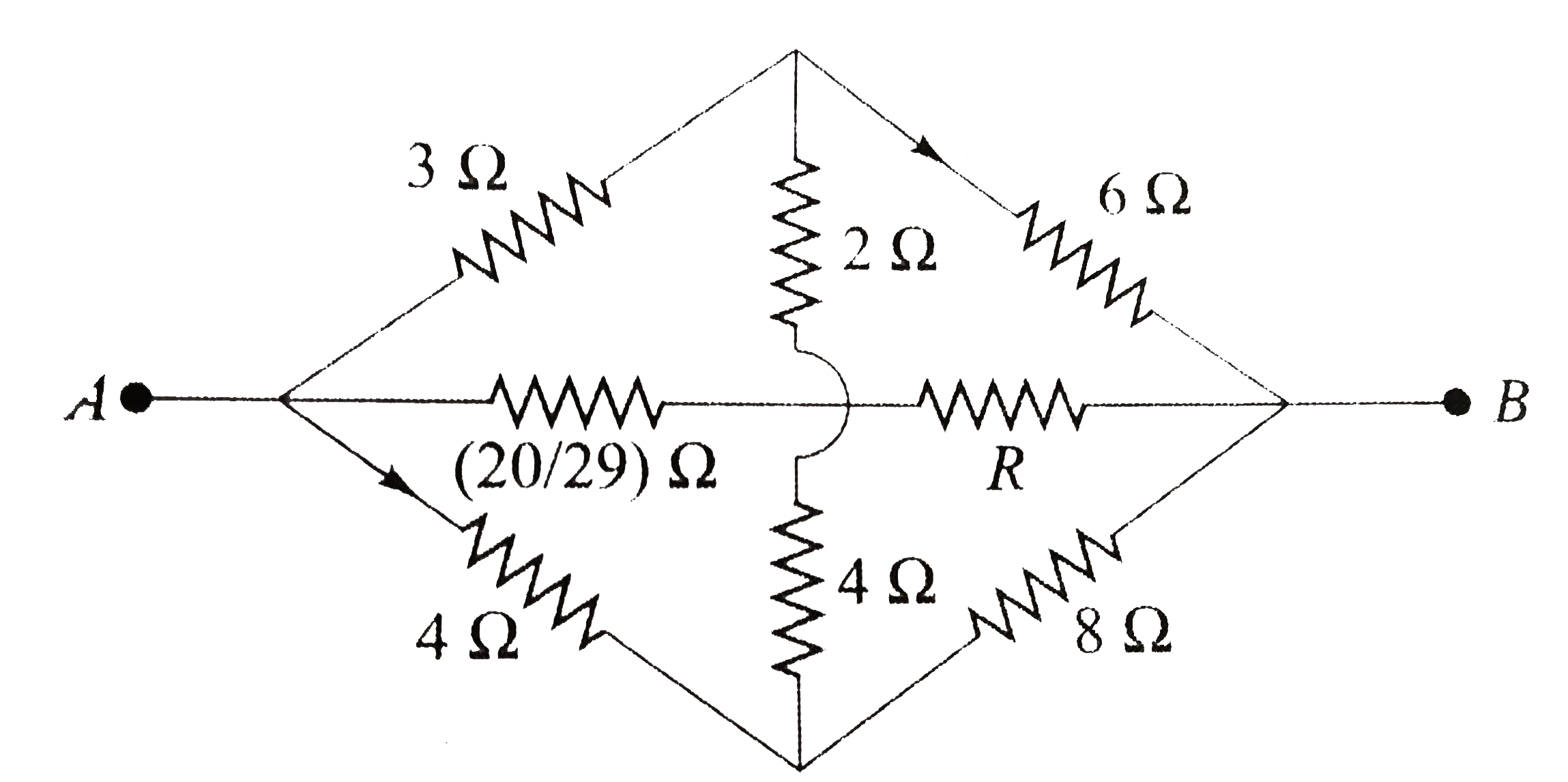 .
.
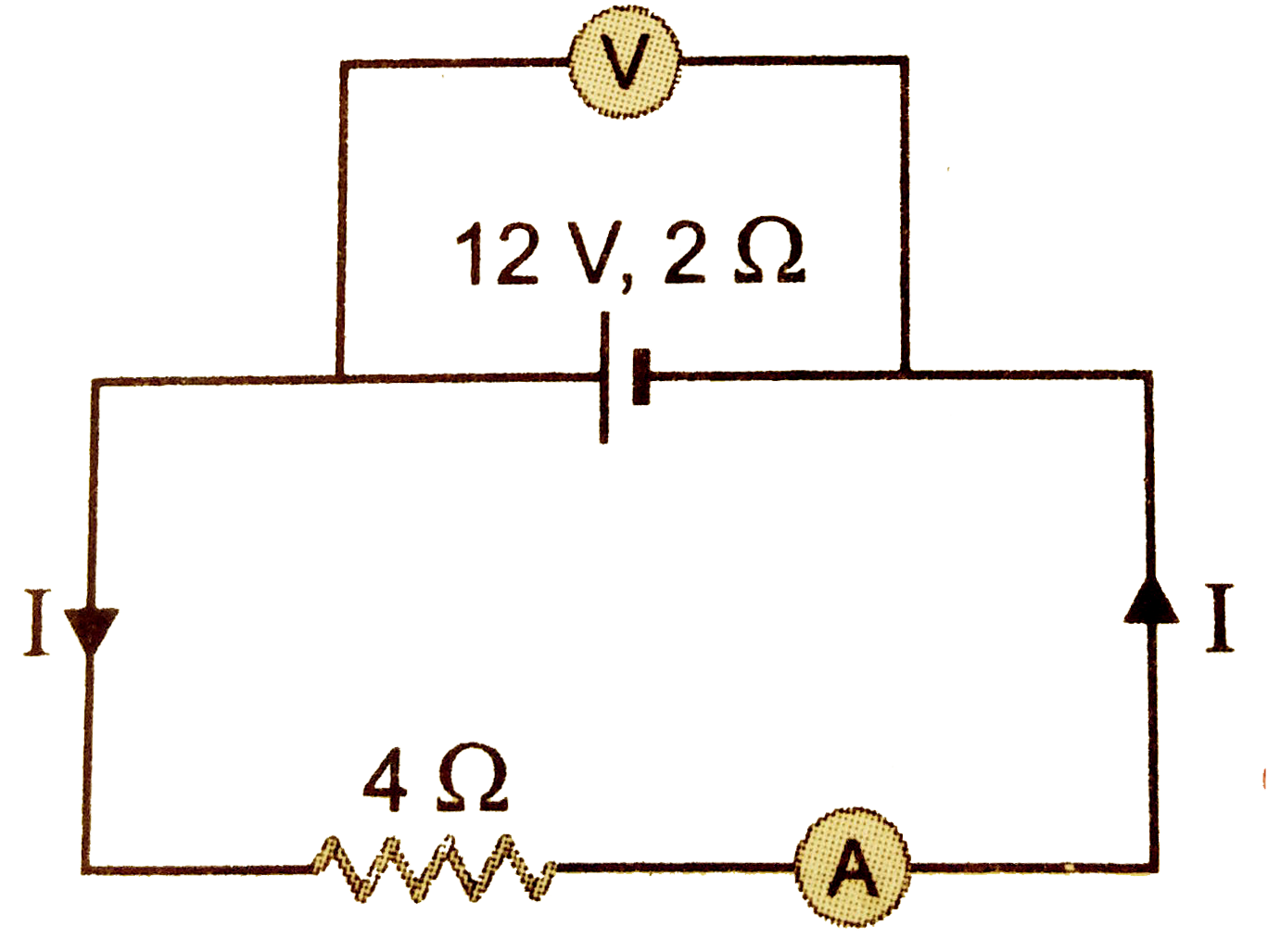
View SolutionA battery of emf 12V and internal resistance 2Ω is connected two a 4Ω resistor. Show that the a voltmeter when placed across cell and across the resistor in turn given the same reading
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the p.d. between the terminals of the battery,
View SolutionFind the amount of silver liberated at cathode if 0.500A of current is passed through AgNO3 electrolyte for 1 hour. Atomic weight of silver s 107.9gmol−1
View SolutionTwo batteries, one of emf 18V and internal resistance 2Ω and the other of emf 12 and internal resistance 1Ω , are connected as shown. The voltmeter V will record a reading of

View SolutionIf three uniform spheres, each having mass M and radius R, are kept in such a way that each touches the other two, the magnitude of the gravitational force on any sphere due to the other two is:
View Solution
