The pressure of an ideal gas is weitten as p=2E3V.Here E refers to
(a)translational kinetic energy
(b)rotational kinetic energy
(c)vibrational kinetic energy
(d)total kinetic energy.
The correct Answer is:A
Step by step video, text & image solution for The pressure of an ideal gas is weitten as p=(2E)/(3V).Here E refers to by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINETIC THEORY OF GASESBOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Objective 2
7 Videos
- KINETIC THEORY OF GASESBOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Exercises
62 Videos
- KINETIC THEORY OF GASESBOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Short Answer
14 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises
19 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
15 Videos
Similar Questions
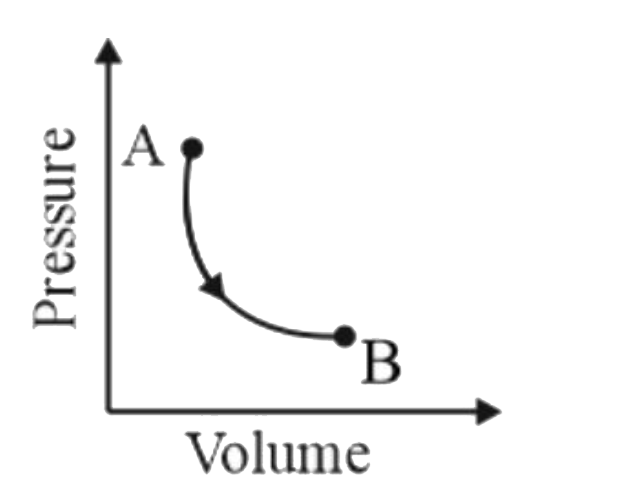
The pressure and volume of an ideal gas are related as pα1v2 for process A→B as shown in figure . The pressure and volume at A are 3p0andv0 respectively and pressure B is p0 the work done in the process A→B is found to be [x−√3]p0v0 find
View SolutionThe K.E. of one mole of an ideal gas is
View Solution
Knowledge Check
The pressure of an ideal gas is written as p=2E3V.Here E refers to
ATranslational kinetic energyBRotational kinetic energyCVibrational kinetic energyDTotal kinetic energy.The pressure of an ideal gas is written as p=2E3V.Here E refers to
Atranslational kineticBrotational kineticCvibrational kineticDinversely proportional to pressureThe pressure P of an ideal gas and its kinetic energy E per unit volume are related as –
AP=12EBP=ECP=35EDP=23E
The energy density uV of an ideal gas is related to its pressure P as
View Solutionvan der Waal's equation for calculating the pressure of a non ideal gas is
(P+an2V2)(V−nb)=nRT
van der Waal's suggested that the pressure exerted by an ideal gas , Pideal, is related to the experiventally measured pressure, Pideal by the equation
Pideal=Preal↑observed pressure+an2V2↑currection term
Constant 'a' is measure of intermolecular interaction between gaseous molecules that gives rise to nonideal behavior. It depends upon how frequently any two molecules approach each other closely. Another correction concerns the volume occupied by the gas molecules. In the ideal gas equation, V represents the volume of the container. However, each molecule does occupy a finite, although small, intrinsic volume, so the effective volume of the gas vecomes (V-nb), where n is the number of moles of the gas and b is a constant. The term nb represents the volume occupied by gas particles present in n moles of the gas .
Having taken into account the corrections for pressure and volume, we can rewrite the ideal gas equation as follows :
(P+an2V2)corrected pressure(V−nb)corrected volume=nRT
The van der Waals' constant 'a' for CO2 gas is greater than that of H2 gas. Its mean that the
View Solutionvan der Waal's equation for calculating the pressure of a non ideal gas is
(P+an2V2)(V−nb)=nRT
van der Waal's suggested that the pressure exerted by an ideal gas , Pideal, is related to the experiventally measured pressure, Pideal by the equation
Pideal=Preal↑observed pressure+an2V2↑currection term
Constant 'a' is measure of intermolecular interaction between gaseous molecules that gives rise to nonideal behavior. It depends upon how frequently any two molecules approach each other closely. Another correction concerns the volume occupied by the gas molecules. In the ideal gas equation, V represents the volume of the container. However, each molecule does occupy a finite, although small, intrinsic volume, so the effective volume of the gas vecomes (V-nb), where n is the number of moles of the gas and b is a constant. The term nb represents the volume occupied by gas particles present in n moles of the gas .
Having taken into account the corrections for pressure and volume, we can rewrite the ideal gas equation as follows :
(P+an2V2)corrected pressure(V−nb)corrected volume=nRT
For non-zero value of force of attraction between gas moleculer at large volume, gas equation will be :
View Solutionvan der Waal's equation for calculating the pressure of a non ideal gas is
(P+an2V2)(V−nb)=nRT
van der Waal's suggested that the pressure exerted by an ideal gas , Pideal, is related to the experiventally measured pressure, Pideal by the equation
Pideal=Preal↑observed pressure+an2V2↑currection term
Constant 'a' is measure of intermolecular interaction between gaseous molecules that gives rise to nonideal behavior. It depends upon how frequently any two molecules approach each other closely. Another correction concerns the volume occupied by the gas molecules. In the ideal gas equation, V represents the volume of the container. However, each molecule does occupy a finite, although small, intrinsic volume, so the effective volume of the gas vecomes (V-nb), where n is the number of moles of the gas and b is a constant. The term nb represents the volume occupied by gas particles present in n moles of the gas .
Having taken into account the corrections for pressure and volume, we can rewrite the ideal gas equation as follows :
(P+an2V2)corrected pressure(V−nb)corrected volume=nRT
AT relatively high pressures, the van der Waals' equation of state reduces to
View SolutionThe pressure p and volume V of an ideal gas both increase in a process.
View Solution
