The principle of 'parallax' in Art. 1(c ).4. is used in the determination of distacne of very distant stars. The baseline AB in the line joining the Earth's two locations six months apart in its orbit around the sun. That is, the baseline is about the diameter of the Earth 's orbit ≈3×1011m. However, even the nearest stars are so distnat thet with such a long baseline, they show parallax only of the order of 1''(second) of arc or so . A parsec is a convenient unit of length on the astronomical scale. It is the distance of an objhect that will shown a parallax of 1'' (second) of arc fome oppsoite ends of a beasline equal to the distance from the Earth to the sun. How much is a parsec in terms of metres ?
Video Solution
Text Solution
From parallax method we can say
θ=b/D, where b = baseline, D = distance of distant object or star
Since, θ=1(s) and n=3×1011m
D=b/20=3×1011/2×4.85×10−6m
or D=3×1011/9.7×10−6m=30×1016/9.7m
3.09×1016m=3×1016m.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If a star is moving towards the earth, then the lines are shifted towards
AredBinfra-redCblueDgreenAssuming that earth and mars move in circular orbits around the sun, with the martian orbit being 1.52 times the orbital radius of the earth. The length of the martian year is days is
A(1.52)2/3×365B(1.52)3/2×365C(1.52)2×365D(1.52)3×365An earth satellite is moving around the earth in circular orbit. IN such case what is conserved
AvelocityBlinear momentumCangular momentumDnone of the above
The mean radius of the earth's orbit round the sun is 1.5×1011 . The mean radius of the orbit of mercury round the sun is 6×1010m. The mercury will rotate around the sun in
View SolutionIn adjoining figure earth goes around the sun in eliptical orbit on which point the orbital speed is maximum :
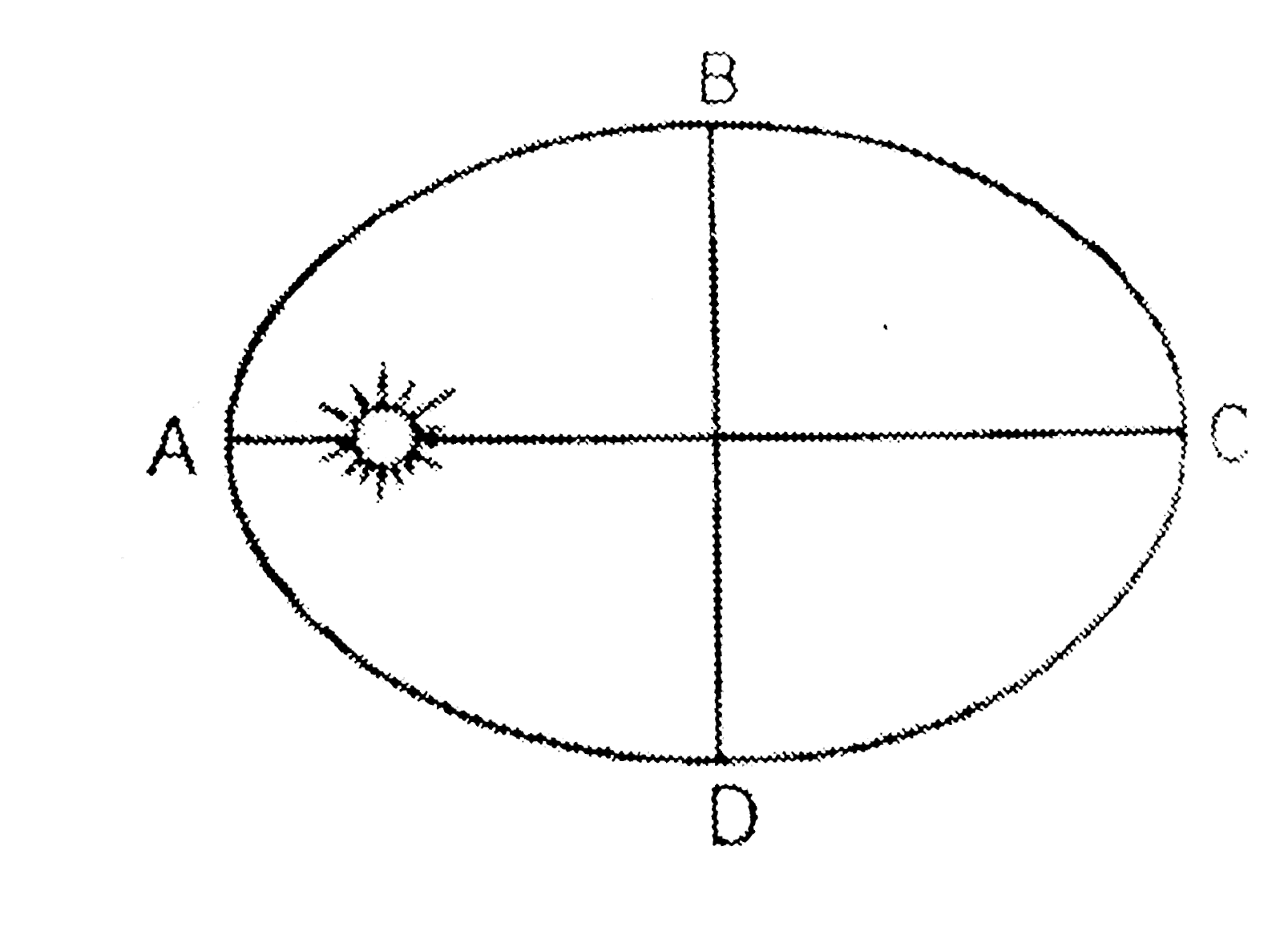
View SolutionSuppose there existed a planet that went around the sun twice as fast as the earth. What would by its orbital size?
View SolutionThe mean orbital radius of the Earth around the Sun is 1.5×108km. Estimate the mass of the Sun.
View SolutionThe sun's angular diameter is measured to be 1920''. The distance of the sun from the earth is 1.496×1011m. What is the diameter of the sun?
View Solution
