The radii and Young's moduli of two uniform wires A and B are in the ratio 2:1 and 1:2 respectively. Both wires are subjected to the same longitudinal force. If the increase in leangth of the wire A is one percent, the percentage increae in length of the wire B is
1.0
1.5
2.0
3.0
The correct Answer is:C
Young's modulus, Y=FLπr2△L
or △LL=Fπr2Y
For the force ,
△LLB△LA△LA=(rArB)2(YAYB)=(21)2(12)=2
△LBLB=2△LALA
LBLB×100=2(△LALA×100)=2%
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - AIIMS Questions
41 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test
29 Videos
Similar Questions
A wire has Piosson's ratio 0.3. If the change in the length of the wire on stretching it is 1% then percentage change in the volume of the wire will be
View SolutionA stress of 1kg/mm2 is applied on a wire. If the modulus of elasticity of the wire is 1010dyne/cm2, then the percentage increase in the length of the wire will be
View Solution
Knowledge Check
The ratio of the lengths of two wires A and B of same material is 1:2 and the ratio of their diameter is 2:1. They are stretched by the same force, then the ratio of increase in length will be
A2:1B1:4C1:8D8:1The ratio of the lengths of two wires A and B of same material is 1:2 and the ratio of their diameters is 2:1. They are stretched by the same force, then the ratio of increase in length will be
A2:1B1:4C1:8D8:1If the ratio of diameters,lengths and Young's moduli of steel and brass wires shown in the figure are p, q and r respectively . Then the corresponding ratio of increase in their lenghts would be
 A3q5p2rB5q3p2rC3q5prD5q3pr
A3q5p2rB5q3p2rC3q5prD5q3pr
If the ratio of lengths, radii and young's modulii of steel and brass wires in the figure are a,b and c, respectively. Then, the corresponding ratio of increase in their lengths would be

View SolutionTwo parallel wires A and B of same meterial are fixed to rigid support at the upper ends and subjected to same load at the lower ends. The subjeted to same load at the lower ends. The lengths of the wire are in the ration 4 : 5 and their radii are in the ratio 4 : 3 the increase in the length of wire A is 1 mm. Calculate the increase in the length of wire A is 1mm. Calculate the increase in the length of the wire B.
View SolutionIf the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a,b and c repectively then the corresponding ratio of increase in their lengths is
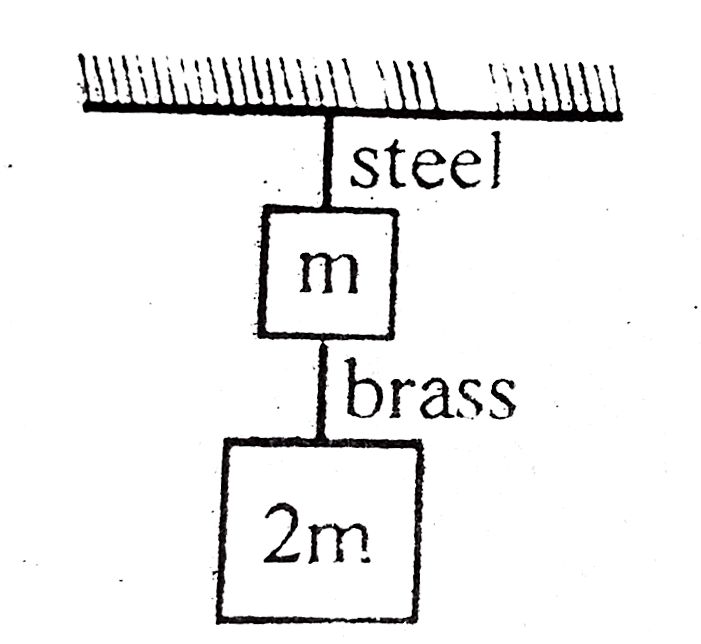
View SolutionThe ratio of diameters of two wires of the same material and same length is n : 1. If the same load is applied to both the wires then the increase in the length of the thin wire is (n>1)
View SolutionA piece of copper wire has twice the radius of a piece of steel wire. Young's modulus for steel is twice that of the copper. One end of the copper wire is joined to one end of the steel wire so that both can be subjected to the same longitudinal force. By what fraction of its length will the steel have stretched when the length of the copper has increased by 1%?
View Solution
