The radius of a planet is R. A satellite revolves around it in a circle of radius r with angular velocity ω0. The acceleration due to the gravity on planet's surface is
Let m be the mass of the satellite. Then,
mrω2=(GMmr2) or GM=ω2r3
Now g=GMR2=ω2r3R2
Topper's Solved these Questions
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - PROBLEMS FOR PRACTIVE B
1 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - PROBLEMS FOR PRACTIVE C
1 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - PROBLEMS FOR PRACTIVE A
1 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Assertion - Reason Type questions
14 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
Similar Questions
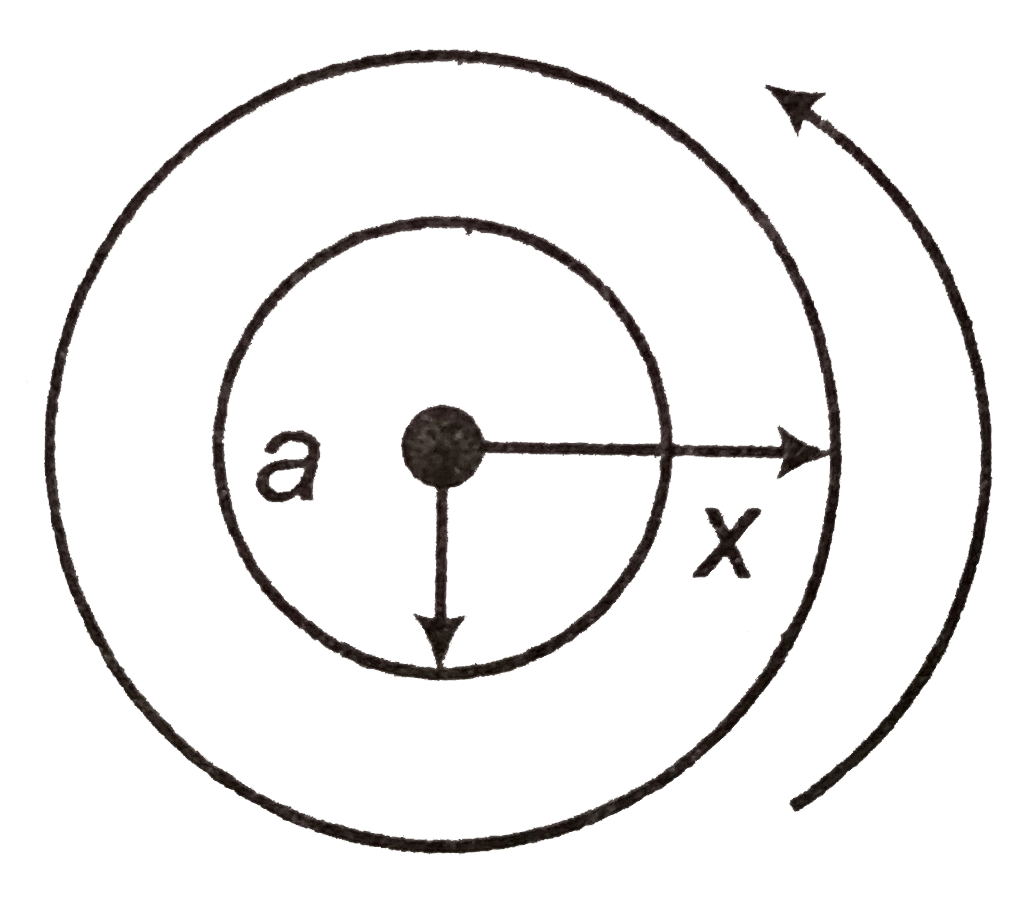
The radius of a planet is a. satelite revolves around it in a circle of radius x with angular velocity ω. The acceleration due to the gravity on planet's surface is
View SolutionThe radius ofa planet is R1and a satellite revolves round it in a circle of radius R2. The tiemperiod of revolution is T. find the acceleration due to the gravitational of the plane at its surface.
View Solution
Knowledge Check
The radius of a planet is n times the radius of earth (R). A satellite revolves around it in a circle of radius 4nR with angular velocity ω. The acceleration due to gravity on planet's surface is
ARω2B16 Rω2C32nRω2D64nRω2The mass of a planet is twice the mass of earth and diameter of the planet is thrie the diameter of the earth, then the acceleration due to gravity on the planet's surface is
Ag/2B2gC2g/9D3g/√2A particle is revolving in a circle of radius r and centre at 'O' with uniform angular velocity ω. Choose the correct option(s) :
 Athe ratio of angular velocity at A about O and about B is 3:2Bthe angular velocity at A about all points O,B and C is same.Cthe angular velocity at A about C is ω/2Dthe velocity at A and C are same.
Athe ratio of angular velocity at A about O and about B is 3:2Bthe angular velocity at A about all points O,B and C is same.Cthe angular velocity at A about C is ω/2Dthe velocity at A and C are same.
A satellite of mass m revolves revolves round the earth of mass M in a circular orbit of radius r with an angular velocity ω. If the angular velocity is ω/8 then the radius of the orbit will be
View SolutionThe radius of a planet is 14 of earth’s radius and its acceleration due to gravity is double that of earth’s acceleration due to gravity. How many times will the escape velocity at the planet’s surface be as compared to its value on earth’s surface
View SolutionIf a planet consists of a satellite whose mass and radius were both half that of the earh, then acceleration due to gravity at its surface would be
View SolutionThe radius of a planet is 14 of earth’s radius and its acceleration due to gravity is double that of earth’s acceleration due to gravity. How many times will the escape velocity at the planet’s surface be as compared to its value on earth’s surface
View SolutionPeriodic time of a satellite revolving above Earth's surface at a height equal to R, radius of Earth, is : [g is acceleration due to gravity at Earth's surface]
View Solution
