The radius ofa planet is R1and a satellite revolves round it in a circle of radius R2. The tiemperiod of revolution is T. find the acceleration due to the gravitational of the plane at its surface.
The correct Answer is:A, B, C, D
T=2π⎛⎜
⎜⎝√R22gR21⎞⎟
⎟⎠
or, T2=4π2R22gR21
or g=4π2T2R22R21
∴ Acceleration due to gravity of the planet is
=4π2T2=R22R21
Topper's Solved these Questions
Similar Questions
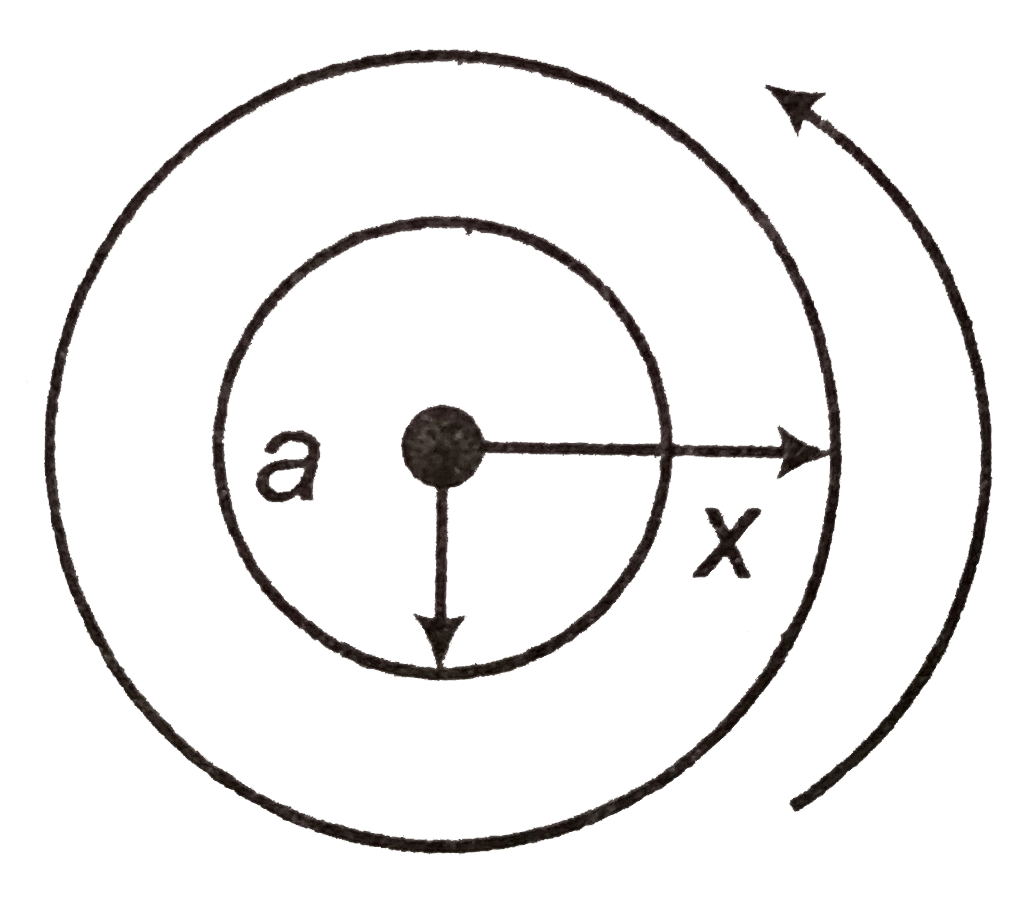
The radius of a planet is a. satelite revolves around it in a circle of radius x with angular velocity ω. The acceleration due to the gravity on planet's surface is
View SolutionTwo satellite of mass m and 9m are orbiting a planet in orbits of radius R. Their periods of revolution will be in the ratio of
View Solution
Knowledge Check
The radius of a planet is R. A satellite revolves around it in a circle of radius r with angular velocity ω0. The acceleration due to the gravity on planet's surface is
Ar3ω0RBr3ω20R2Cr3ω20RDr3ω20R2The radius of a planet is n times the radius of earth (R). A satellite revolves around it in a circle of radius 4nR with angular velocity ω. The acceleration due to gravity on planet's surface is
ARω2B16 Rω2C32nRω2D64nRω2An artificial satellite of mass m is revolving round the earth in a circle of radius R. Then work done in one revolution is
AmgRBmgR2C2πR×mgDzero
Radius of a geostationary satellite revolving round the earth is 'r'. Then period of revolution of another satellite revolving in an orbit of radius r/2 is
View SolutionA satellite of mass m revolves around the earth of radius R at a height x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
View SolutionA satellite of mass m revolves around the earth of radius R at a hight x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
View SolutionImagine a light planet revolving around a very massive star in a circular orbit of radius R with a period of revolution T. If the gravitational force of attraction between the planet and the star is proportional to R−5/2, then T2 is proportional to
View SolutionImagine a light planet revolving around a vary massive star in a circular orbit of radius R with a period of revolution T. if the gravitational force of attraction between planet and star is proportional to R−5/2, then T2 is proportional to
View Solution
