The rate of heat radiation from two patches of skin each of area S, on a patient's chest differ by 2%. If the patch of the lower temperature is at 300 K and the emissivity of both the patches is assumed to be unity, the temperature of the other patch is closest to
301.5 K
306 K
308. 5 K
312 K
The correct Answer is:A
To solve the problem, we will use the Stefan-Boltzmann law, which states that the rate of heat radiation (E) from a surface is proportional to the fourth power of its absolute temperature (T). The formula is given by:
E=SσT4
where:
- E is the rate of heat radiation,
- S is the area of the surface,
- σ is the Stefan-Boltzmann constant,
- T is the absolute temperature in Kelvin.
1. Identify the given information:
- Temperature of the lower patch, T1=300K
- The difference in heat radiation between the two patches is 2%, which can be expressed as:
E2−E1E1=0.02
2. Express the heat radiation for both patches:
- For the first patch (lower temperature):
E1=SσT41
- For the second patch (higher temperature):
E2=SσT42
3. Set up the equation based on the percentage difference:
- Substitute E1 and E2 into the percentage difference equation:
SσT42−SσT41SσT41=0.02
4. Simplify the equation:
- Cancel out Sσ from the numerator and denominator:
T42−T41T41=0.02
- Rearranging gives:
T42−T41=0.02T41
5. Substitute T1 into the equation:
- Substitute T1=300K:
T42−(300)4=0.02×(300)4
6. Calculate (300)4:
- (300)4=8.1×108
- Therefore:
T42−8.1×108=0.02×8.1×108
- Calculate 0.02×8.1×108=1.62×107.
7. Rearranging gives:
- T42=8.1×108+1.62×107
- T42=8.256×108
8. Taking the fourth root:
- To find T2:
T2=(8.256×108)1/4
- This calculation results in:
T2≈301.5K
Conclusion:
The temperature of the other patch is closest to 301.5 K.
- E is the rate of heat radiation,
- S is the area of the surface,
- σ is the Stefan-Boltzmann constant,
- T is the absolute temperature in Kelvin.
- Temperature of the lower patch, T1=300K
- The difference in heat radiation between the two patches is 2%, which can be expressed as:
E2−E1E1=0.02
- For the first patch (lower temperature):
E1=SσT41
- For the second patch (higher temperature):
E2=SσT42
- Substitute E1 and E2 into the percentage difference equation:
SσT42−SσT41SσT41=0.02
- Cancel out Sσ from the numerator and denominator:
T42−T41T41=0.02
- Rearranging gives:
T42−T41=0.02T41
- Substitute T1=300K:
T42−(300)4=0.02×(300)4
- (300)4=8.1×108
- Therefore:
T42−8.1×108=0.02×8.1×108
- Calculate 0.02×8.1×108=1.62×107.
- T42=8.1×108+1.62×107
- T42=8.256×108
- To find T2:
T2=(8.256×108)1/4
- This calculation results in:
T2≈301.5K
The temperature of the other patch is closest to 301.5 K.
Topper's Solved these Questions
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OSCILLATIONS
23 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - WAVES
98 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - THERMAL CONDUCTION
17 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
24 Videos
- DIMENSIONSBOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)
9 Videos
Similar Questions
A cylinder closed at both ends is separated into two equal parts (45 cm each) by a piston impermeable to heat. Both the parts contain the same masses of gas at a temperature of 300 K and a pressure of 1 atm. If now the gas in one of parts is heated such that the piston shifts by 5 cm, then the temperature and the pressure of the gas in this part after heating is
View SolutionA Carnot refrigerator works between two temperatures of 300 K & 600 K. Find the COP of the refrigerator if heat removed from lower temperature in 300 J.
View Solution
Knowledge Check
The figure show a cross-section of a double glass unit of a window on a vertical wall. A graph wall. A graph of the temperature at different points within the unit is show next to it. The temperature difference across the unit is 13K. It has a crossp-sectional area of 1.3m2 and the rate of heat flow through it is 65W. Then the correct statement is (Glass has a thermal conductivity of 1Wm−1K−1)
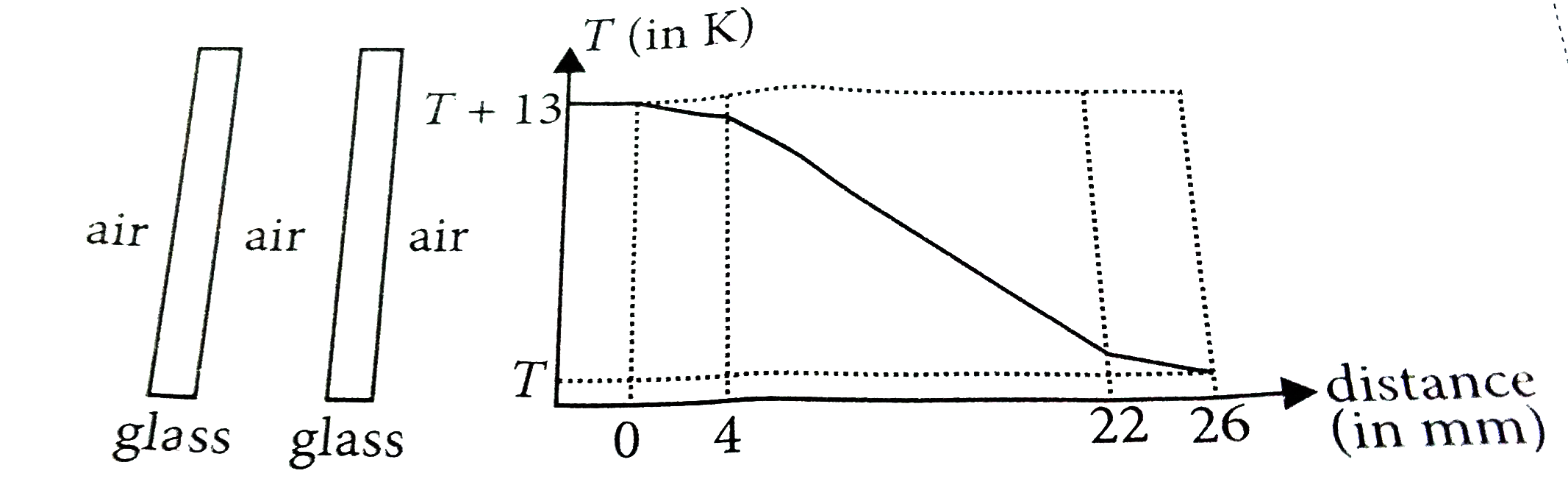 AThe unit is in steady state and in thermal equilibriumBThe unit is in steady state but not in thermal equalibrium.CThe unit is not in steady state but is in thermalDThe unit neither in steady state nor in thermal equilibrium
AThe unit is in steady state and in thermal equilibriumBThe unit is in steady state but not in thermal equalibrium.CThe unit is not in steady state but is in thermalDThe unit neither in steady state nor in thermal equilibriumTwo chunks of metal with heat capacities C1 and C2, are interconnected by a rod length l and cross-sectional area S and fairly low heat conductivity K. The whole system is thermally insulated from the environment. At a moment t=0 the temperature difference betwene the two chunks of metal equals (ΔT)0. Assuming the heat capacity of the rod to be negligible, find the temperature difference between the chucks as a function of time.
AT0exp(−KA(C1+C2)tC1C2)BT0exp(−KA(C1+C2)C1C2)CT0exp(KA(C1+C2)tC1C2)DT0exp(KA(C1+C2)t2C1C2)
The surface of a household radiator has an emissivity of 0.55 and an area of 1.5m2.
(a) At what rate is radiation emitted by the radiator when its temperature is 50∘C?
(b) At what rate is the radiation absorbed by the radiator when the walls of the room are at 22∘C? (c ) What is the net rate of radiation from the radiator? (stefan constant σ=6×10−8W/m2−K4)
View SolutionA metal block of heat capacity 90J/.∘C placed in a room at 25∘C is heated electrically. The heater is switched off when the temperature reaches 35∘C. The temperature of the block rises at the rate of 2∘C/s just after the heater is switched on and falls at the rate of 0.2∘C/s just after the heater is switched off. Assume Newton's law of cooling to hold (a) Find the power of the heater. (b) Find the power radiated by the block just after the heater is switched off. (c ) Find the power radiated by the block when the temperature of the block is 30∘C. (d) Assuming that the power radiated at 30∘C respresents the average value in the heating process, find the time for which the heater was kept on.
View SolutionImagine a system, that can keep the room temperature within a narrow range between 20∘C to 25∘C. The system includes a heat engine operating with variable power P = 3KT, where K is a constant coefficient, depending upon the thermal insulation of the room, the area of the walls and the thickness of the walls. T is temperature of the room in temperature drops lower than 20∘C, the engine turns on, when the temperature increase over 25∘C, the engine turns off, room looses energy at a rate of K(T−T0),T0 is the outdoor temperature. The heat capacity of the room is C.
Given (T0=10∘C,ln(32)=0.4,ln(65)=0.18,CK=750 SI-unit)
Suppose at t = 0, the engine turns off, after how much time interval, again, the engine will turn on
View SolutionImagine a system, that can keep the room temperature within a narrow range between 20∘C to 25∘C. The system includes a heat engine operating with variable power P = 3KT, where K is a constant coefficient, depending upon the thermal insulation of the room, the area of the walls and the thickness of the walls. T is temperature of the room in temperature drops lower than 20∘C, the engine turns on, when the temperature increase over 25∘C, the engine turns off, room looses energy at a rate of K(T−T0),T0 is the outdoor temperature. The heat capacity of the room is C.
Given (T0=10∘C,ln(32)=0.4,ln(65)=0.18,CK=750 SI-unit)
Suppose at t = 0, the engine turns on, after how much time interval again, the engine will turn off
View SolutionWhat is the heat lost from the body of a person her hour whose body temperature is 37∘C and the surrounding temperature is 20∘C ? The emissivity of the skin is 0.92 and the surface area of skin is 1.6m2 . (Asssume that the person is unclothed.)
View SolutionTwo conducting cylinders of equal length but different radii are connected in series between two heat baths kept at temperatures T1=300KandT2=100K, as shown in the figure. The radius of the bigger cylinder is twice that of the smaller one and the thermal conductivities of the materials of the smaller and the larger cylinders are K1andK2 respectively. If the temperature at the junction of the two cylinders in the steady state is 200 K, then K1/K2=__________.
View Solution
