The ratio between velocity of light in vacuum to velocity of light in air is called refractive index. ____
To solve the question regarding the refractive index, we can break it down into the following steps:
1. Understanding the Definition of Refractive Index:
- The refractive index (n) is defined as the ratio of the speed of light in a vacuum (c) to the speed of light in a medium (v). Mathematically, it is expressed as:
n=cv
2. Identifying the Medium:
- In this case, the medium is specified as air.
3. Velocity of Light in Different Mediums:
- The speed of light in a vacuum (c) is approximately 3×108 m/s.
- The speed of light in air (v) is very close to that in a vacuum, approximately 3×108 m/s as well, but slightly less due to the presence of air molecules.
4. Calculating the Refractive Index for Air:
- Since the speed of light in air is nearly equal to that in a vacuum, we can say:
nair=cv≈3×108 m/s3×108 m/s=1
5. Conclusion:
- Therefore, the statement "The ratio between the velocity of light in vacuum to the velocity of light in air is called refractive index" is correct, and specifically, the refractive index of air is approximately equal to 1.
Final Answer:
Yes, the statement is correct. The ratio between the velocity of light in vacuum to the velocity of light in air is called the refractive index, and for air, it is approximately equal to 1.
---
- The refractive index (n) is defined as the ratio of the speed of light in a vacuum (c) to the speed of light in a medium (v). Mathematically, it is expressed as:
n=cv
- In this case, the medium is specified as air.
- The speed of light in a vacuum (c) is approximately 3×108 m/s.
- The speed of light in air (v) is very close to that in a vacuum, approximately 3×108 m/s as well, but slightly less due to the presence of air molecules.
- Since the speed of light in air is nearly equal to that in a vacuum, we can say:
nair=cv≈3×108 m/s3×108 m/s=1
- Therefore, the statement "The ratio between the velocity of light in vacuum to the velocity of light in air is called refractive index" is correct, and specifically, the refractive index of air is approximately equal to 1.
Yes, the statement is correct. The ratio between the velocity of light in vacuum to the velocity of light in air is called the refractive index, and for air, it is approximately equal to 1.
Topper's Solved these Questions
- LIGHT ENERGYBOOK - ICSECHAPTER - LIGHT ENERGYEXERCISE - EXERCISE-5.3 (Objective Type Questions) D. Tick the most appropriate answer.
5 Videos
- LIGHT ENERGYBOOK - ICSECHAPTER - LIGHT ENERGYEXERCISE - EXERCISE-5.3 (Objective Type Questions) E. Match the statements in column A, with those in Column B.
1 Videos
- LIGHT ENERGYBOOK - ICSECHAPTER - LIGHT ENERGYEXERCISE - EXERCISE-5.3 (Objective Type Questions) B. Statements given below are incorrect. Write the correct statements.
5 Videos
- HEAT TRANSFER BOOK - ICSECHAPTER - HEAT TRANSFER EXERCISE - Picture Study
2 Videos
- MATTER BOOK - ICSECHAPTER - MATTER EXERCISE - THEME ASSIGNMENT
25 Videos
Similar Questions
The ratio of velocity of light in vacuum to the velocity of light in a given media is called ______.
View SolutionVelocity of light is equal to
View SolutionThe ratio between the velocity of light in a given optical medium to the velocity of light in vacuum is called refractive index.
View SolutionIf c is velocity of light in vacuum and v is the velocity of light in a medium of refractive index μ, then
View SolutionThe ratio of the speed of light in air to the speed of light in another medium
View SolutionHow is the refractive index of a material related to:
Velocity of light in vacuum or air and the velocity of light in a given medium?
View SolutionIf the wavelength of light in vacuum be λ, the wavelength in a medium of refractive index n will be
View SolutionA student when discussing the properties of a medium ( except vaccum) writes
Velocity of light in vaccum = Velocity of light in medium
This formula is
View SolutionA ray of light is incident on a medium with angle of incidence I and refracted into a second medium with angle of refraction r. The graph of sin(i)vssin(R) is as shown in figure. Then the velocity of light in the first medium in n times the velocity of light in the second medium. What shoul be th evalue of n?
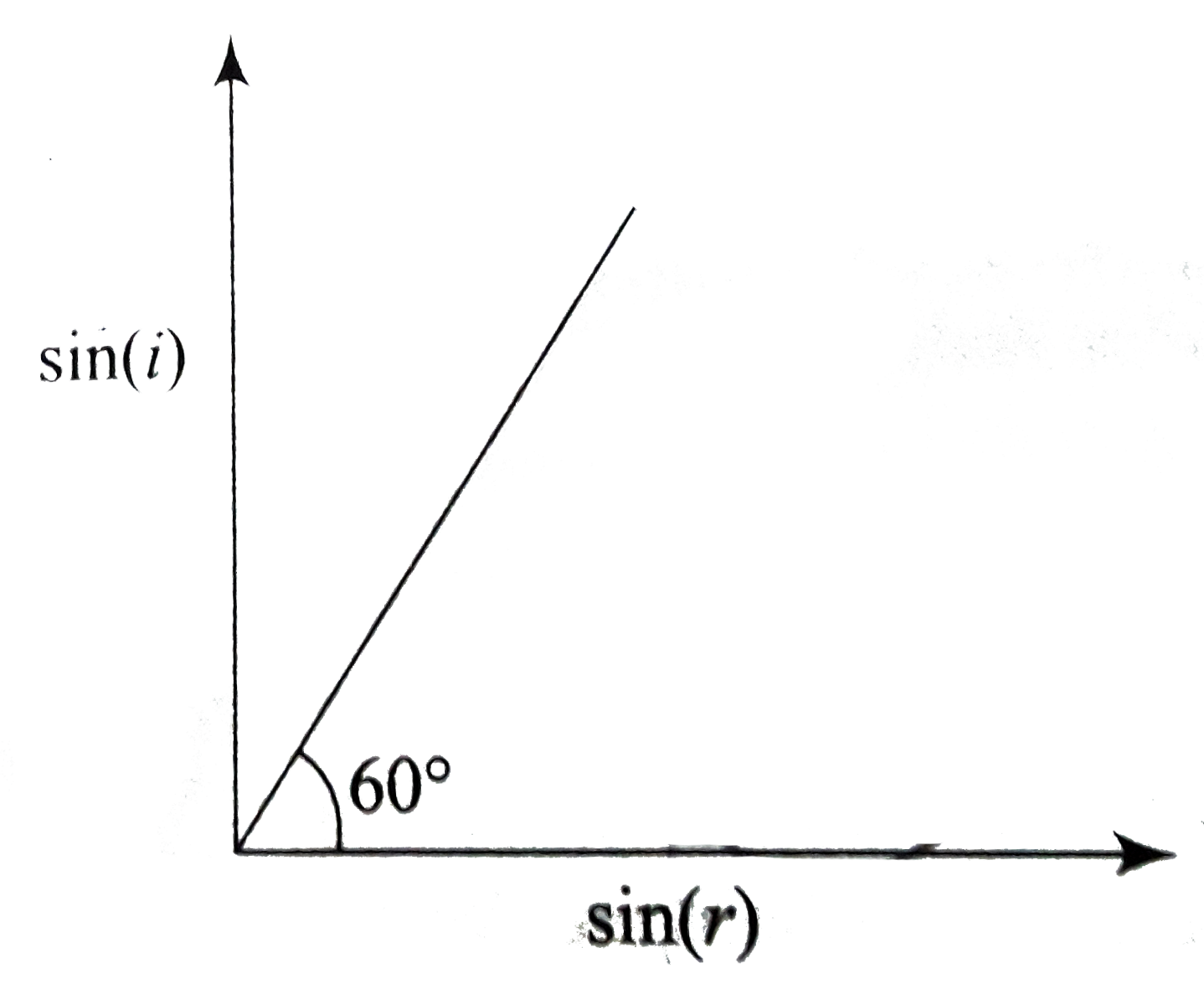
View SolutionThe wavelength of light in vacuum is 6000A∘ and in a medium it is 4000A∘ The refractive index of the medium is:
View Solution
