The ratio of the distance carried away by the water current, downstream, in crossing a river, by a person, making same angle with downstream and upstream is 2:1. The ratio of the speed of person to the water current cannot be less than.
1/3
4/5
2/5
4/3
The correct Answer is:A
(a) Motion of the person making an angle (say prop) with the downstream.
The time taken to cross the river =dvsin∝
The distance carried away downstream in the same time = speed xx time.
x1=(u+vcos∝)dvsin∝ ....(i)
Motion of the person making ∝ angle with upstream.
The time taken to cross the river is equal to dvsin∝
Distance carried away downstream in the same time
x2=[u+vcos(180∘−∝)]dvsin∝
⇒x2=(u−vcosα)dvsinα ...(ii)
given (u+vcos∝)dvsin∝(u−vcos∝)dvsin∝=21
(u+vcos∝)(u−vcos∝)=21⇒3vcos∝=u
⇒vu=sec∝3
sec∝≥1⇒sec∝3≥13
From Eq. (iii),vu≥13
So, v/u cannot be less than 1/3,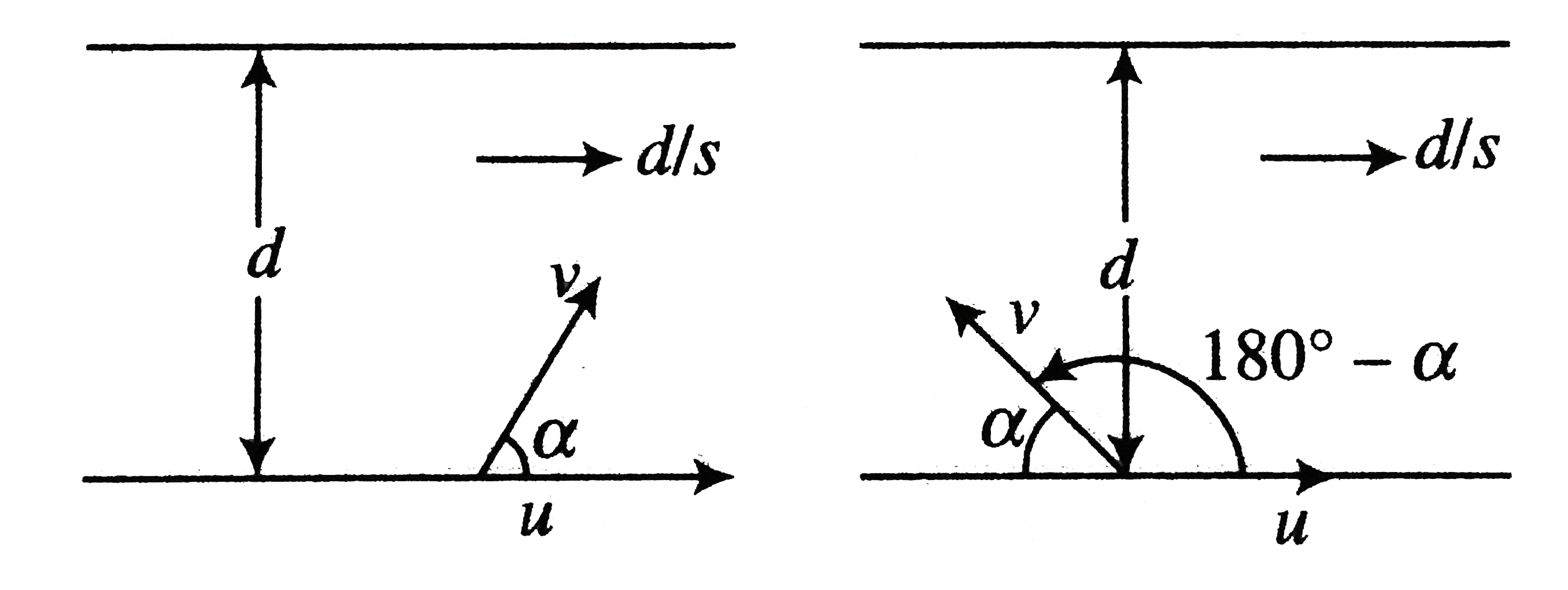
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning
5 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective
40 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
Knowledge Check
The ratio of downstream drift of a person in crossing a river making same angles with downstream and upstream are respectively 2 : 1. The ratio of the speed of river u and the swimming speed of person v is:
Auv=12Buv≤12Cuv≥13Duv≤3A boat takes half time in moving a certain distance downstream than upstream. The ratio of the speed of the boat in still water and that of the stream is :
A2:1B1:2C4:3D3:1A boat takes half time in moving a certain distance downstream than upstream. The ratio of the speed of the boat in still water and that of the stream is :
A2:1B1:2C4:3D3:1
A boat travels a distance of 50 km downstream in 5 h and 80 km upstream in 10 h. Find the speed of the boat and speed of the current.
View SolutionA person, intending to cross a river by the shortest path, starts at an angle ∝ with the downstream. If the speed of the person be less than that of water current, show that ∝ must be obtuse.
View SolutionIshwar is rowing a boat. He takes half time in moving a certain distance downstream than upstream. What is the ratio of the rate of boat in still water to the rate of current?
View SolutionA boat moves downstream at 1 km in 5 min and upstream at 1 km in 12 min what is the speed of the current?
View SolutionRavi can row downstream at 9 km/h and upstream at 5 km/h. Find the speed of Ravi in still water and speed of current.
View Solution
